Here, you will learn various trigonometric identities for class 10th and formulas of trigonometry.
Let’s begin-
In a right angle triangle
sin\(\theta\) = \(p\over h\); cos\(\theta\) = \(b\over h\); tan\(\theta\) = \(p\over b\); cosec\(\theta\) = \(h\over p\); sec\(\theta\) = \(h\over b\) and cot\(\theta\) = \(b\over p\)
where ‘p’ is perpendicular ; ‘b’ is base and ‘h’ is hypotenuse.
Signs of Trigonometric functions in different quadrants
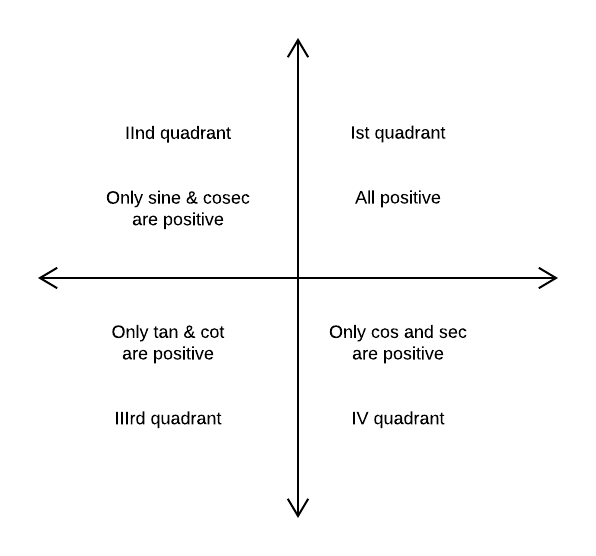
Basic Trigonometric Identities for Class 10th :
(1) \(sin\theta\).\(cosec\theta\) = 1
(2) \(cos\theta\).\(sec\theta\) = 1
(3) \(tan\theta\).\(cot\theta\) = 1
(4) \(tan\theta\) = \(sin\theta\over{cos\theta}\) \(cot\theta\) = \(cos\theta\over{sin\theta}\)
(5) \(sin^2\theta\) + \(cos^2\theta\) = 1
(6) \(sec^2\theta\) – \(tan^2\theta\) = 1
(7) \(cosec^2\theta\) – \(cot^2\theta\) = 1
Trigonometric Ratios of the sum & difference of two angles :
(1) sin(A + B) = sin A cos B + cos A sin B
(2) sin(A – B) = sin A cos B – cos A sin B
(3) cos(A + B) = cos A cos B – sin A sin B
(4) cos(A – B) = cos A cos B + sin A sin B
(5) tan(A + B) = \(tan A + tan B\over {1 – tan A tan B}\)
(6) tan(A – B) = \(tan A – tan B\over {1 + tan A tan B}\)
(7) cot(A + B) = \(cot B cot A – 1\over {cot B + cot A}\)
(8) cot(A – B) = \(cot B cot A + 1\over {cot B – cot A}\)
Formulae to transform the product into sum or difference :
(i) 2 sin A cos B = sin(A + B) + sin(A – B)
(ii) 2 cos A sin B = sin(A + B) – sin(A – B)
(iii) 2 cos A cos B = cos(A + B) – cos(A – B)
(iv) 2 sin A sin B = cos(A – B) – cos(A + B)
Formulae to transform the sum or difference into product :
(i) sin C + sin D = 2 sin(\(C + D\over 2\)) cos(\(C – D\over 2\))
(ii) sin C – sin D = 2 cos(\(C + D\over 2\)) sin(\(C – D\over 2\))
(iii) cos C + cos D = 2 cos(\(C + D\over 2\)) cos(\(C – D\over 2\))
(iv) cos C – cos D = 2 sin(\(C + D\over 2\)) sin(\(D – C\over 2\))
Trigonometric ratios of sum of more than two angles :
(i) sin(A + B + C) = sinAcosBcosC + sinBcosAcosC + sinCcosAcosB – sinAsinBsinC
(ii) cos(A + B + C) = cosAcosBcosC – sinAsinBcosC – sinAcosBsinC – cosAsinBsinC
(iii) tan(A + B + C) = \(tanA + tanB + tanC – tanAtanBtanC\over {1 – tanAtanB – tanBtanC – tanCtanA}\)
Trigonometric ratios of mutiple angles :
(i) sin2A = 2sinAcosA = \(2tanA\over {1+tan^2A}\)
(ii) cos2A = \(cos^2A\) – \(sin^2A\) = \(2cos^2A\) – 1 = 1 – \(2sin^2A\) = \(1 – tan^2A\over {1 + tan^A}\)
(iii) 1 + cos2A = \(2cos^2A\)
(iv) 1 – cos2A = \(2sin^2A\)
(v) tanA = \(1 – cosA\over {sin2A}\) = \(sin2A\over {1+cos2A}\)
(vi) tan2A = \(2tanA\over {1-tan^2A}\)
(vii) sin3A = 3sinA – \(4sin^3A\)
(viii) cos3A = \(4cos^3A\) – 3cosA
(ix) tan3A = \(3tanA – tan^3A\over {1 – 3tan^2A}\)
