Here, you will learn graph of trigonometric functions and domain & range of trigonometric functions.
Graph of Trigonometric Functions :
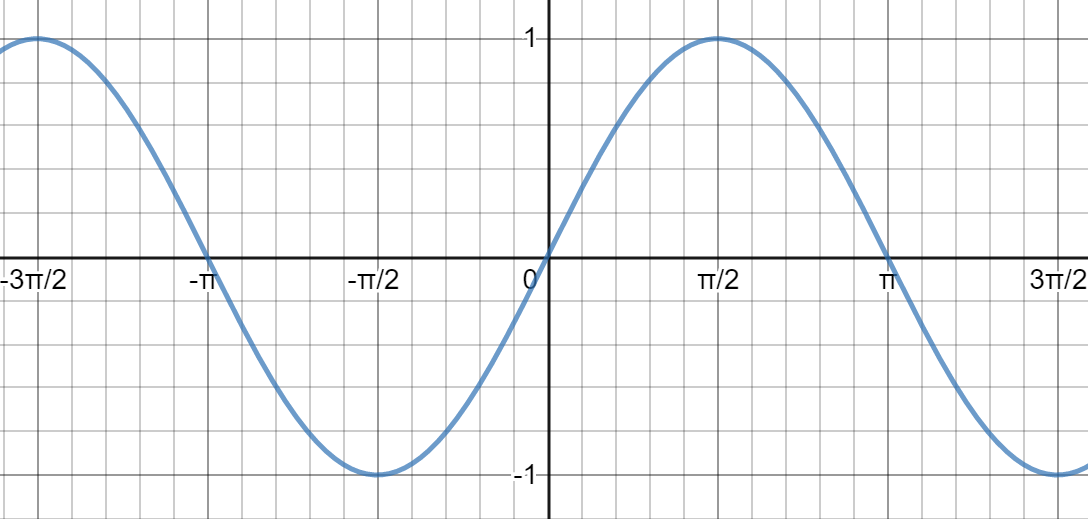
y = sinx
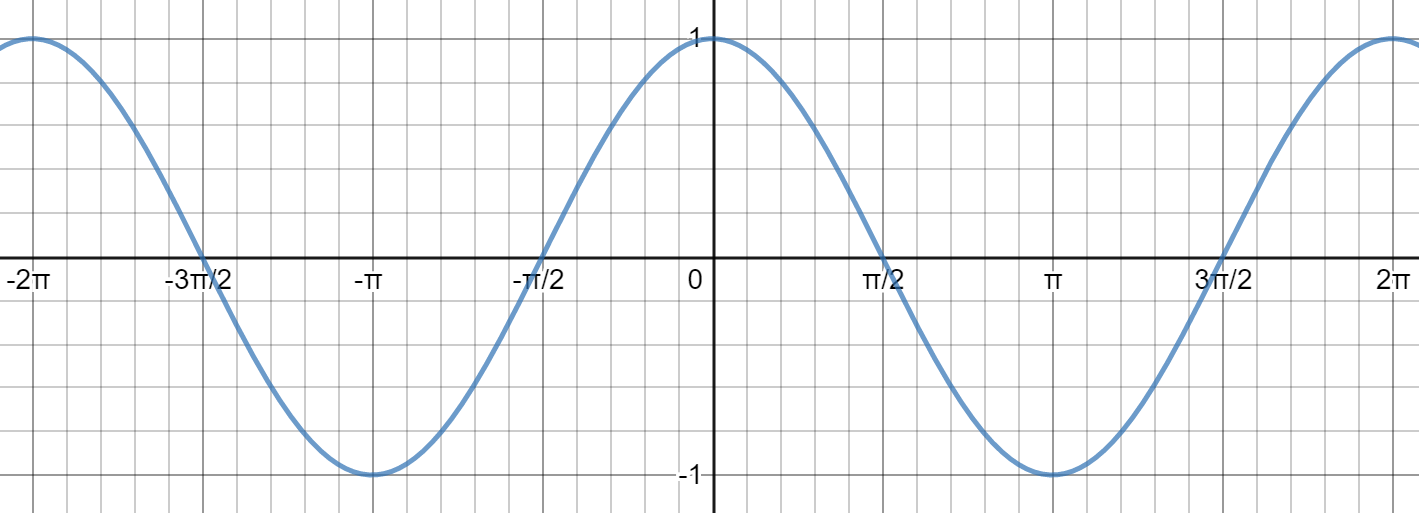
y = cosx
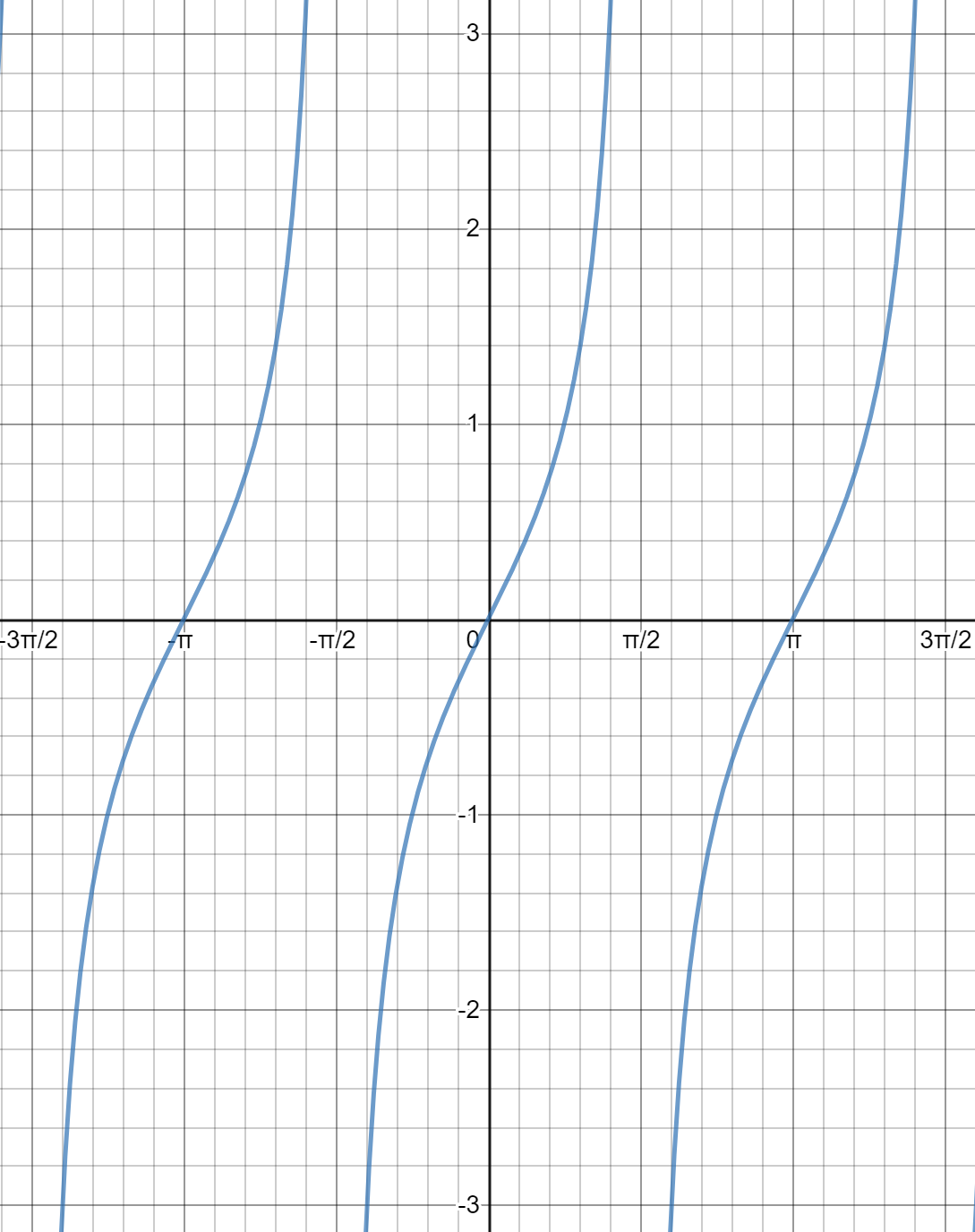
y = tanx
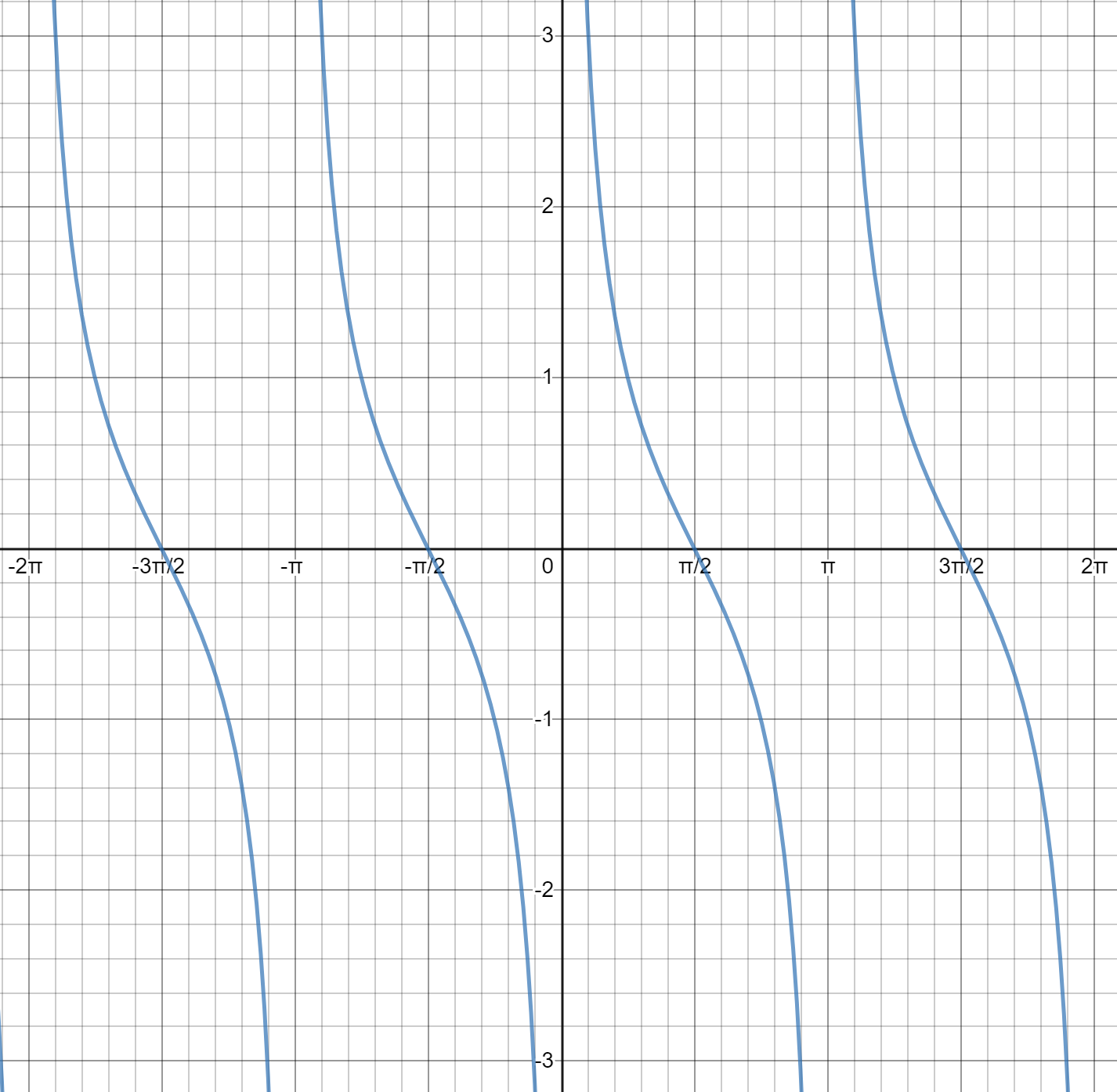
y = cotx
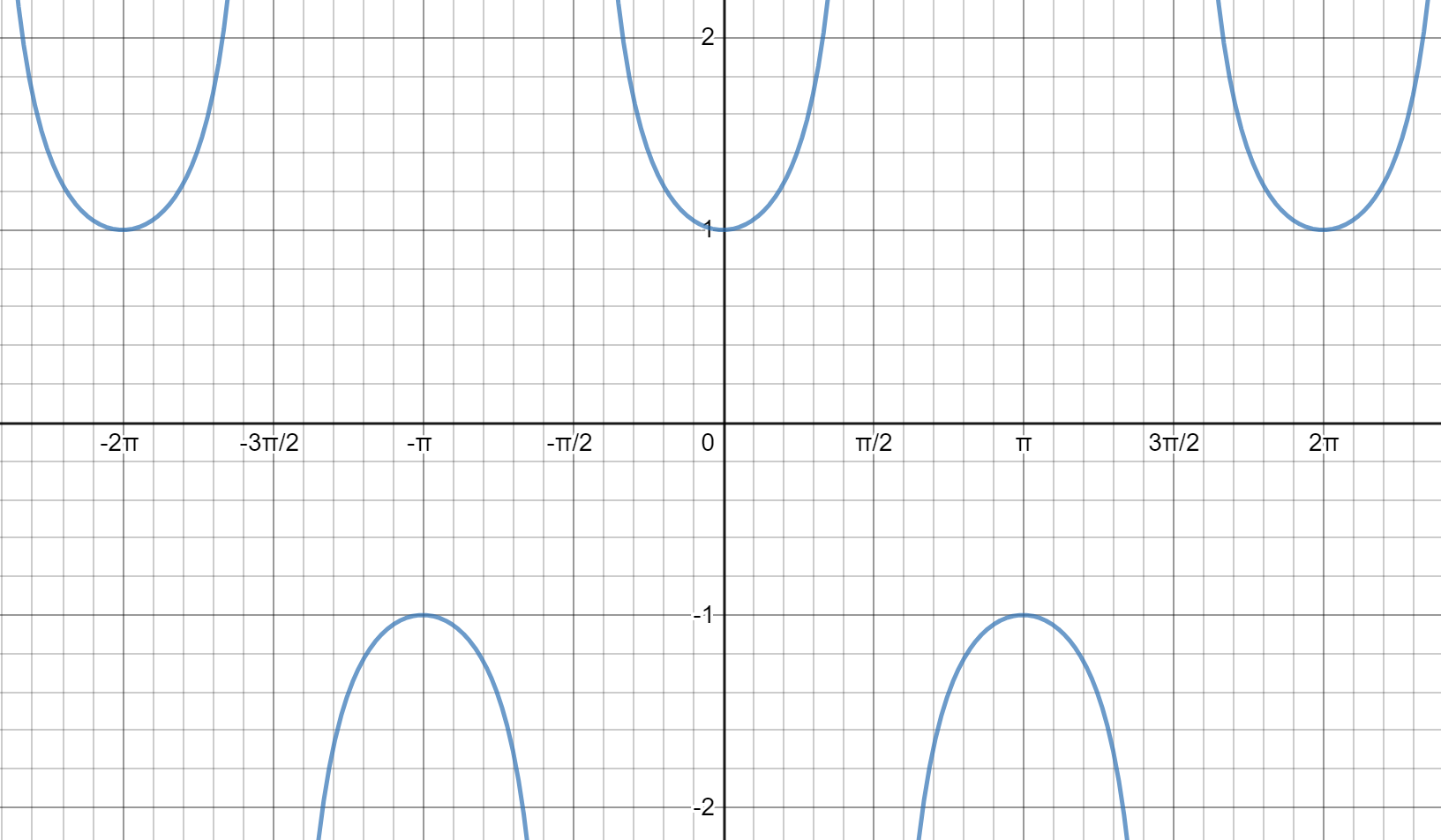
y = secx
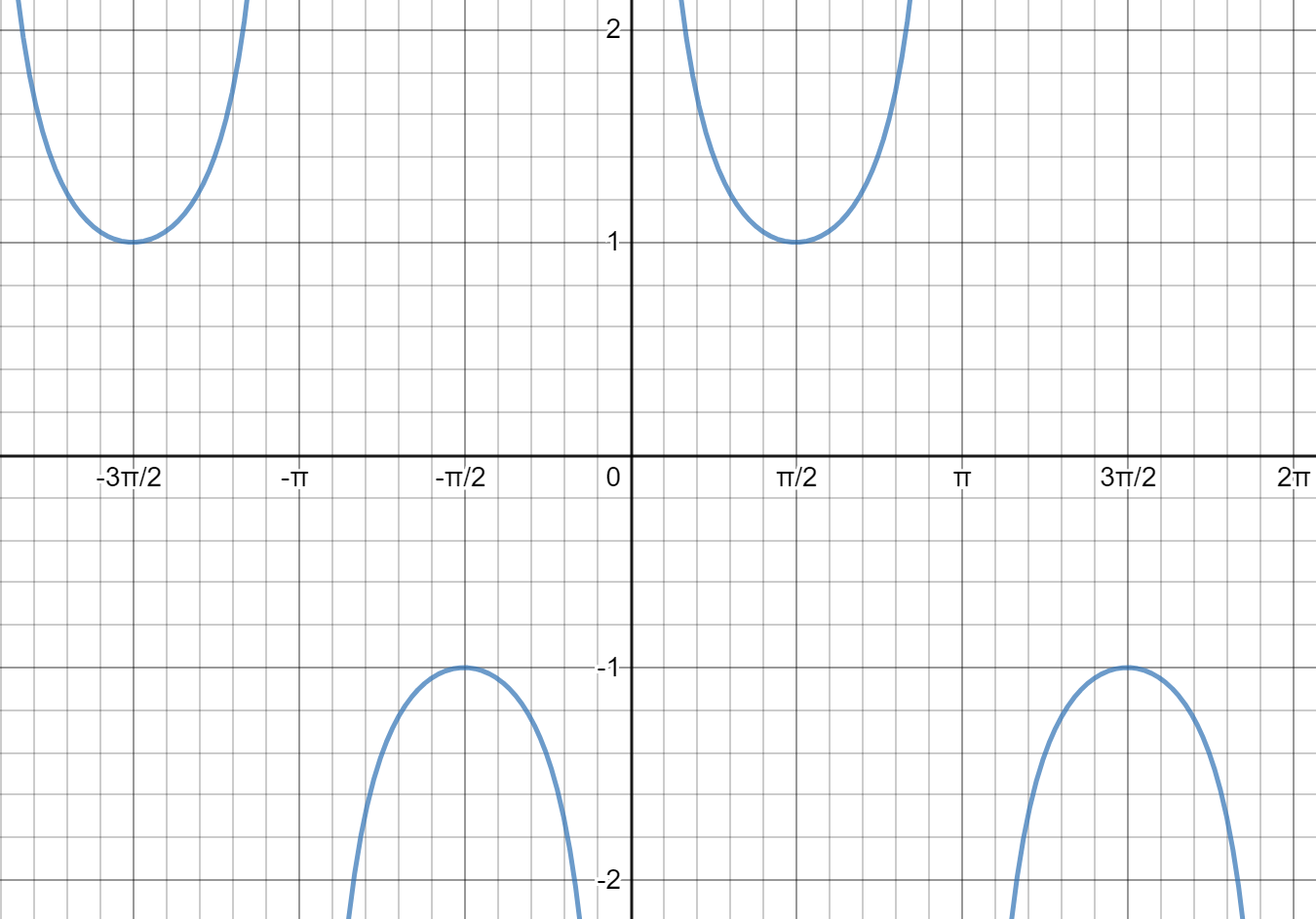
y = cosecx
Values of T-Ratio of some standard angles
| Angles T-Ratio |
0 | \(\pi\over 6\) | \(\pi\over 4\) | \(\pi\over 3\) | \(\pi\over 2\) | \(\pi\) |
| \(sin\theta\) | 0 | \(1\over 2\) | \(1\over \sqrt{2}\) | \(\sqrt{3}\over 2\) | 1 | 0 |
| \(cos\theta\) | 1 | \(\sqrt{3}\over 2\) | \(1\over \sqrt{2}\) | \(1\over 2\) | 0 | -1 |
| \(tan\theta\) | 0 | \(1\over \sqrt{3}\) | 1 | \(\sqrt{3}\) | N.D | 0 |
| \(cot\theta\) | N.D | \(\sqrt{3}\) | 1 | \(1\over \sqrt{3}\) | 0 | N.D |
| \(sec\theta\) | 1 | \(2\over \sqrt{3}\) | \(\sqrt{2}\) | 2 | N.D | -1 |
| \(cosec\theta\) | N.D | 2 | \(\sqrt{2}\) | \(2\over \sqrt{3}\) | 1 | N.D |
N.D = Not defined
Domain, Ranges and Periodicity of Trigonometric function
| T-Ratio | Domain | Range | Period |
| sin x | R | [-1, 1] | \(2\pi\) |
| cos x | R | [-1, 1] | \(2\pi\) |
| tan x | R – {(2n+1)\(\pi/2\); n \(\in\) I} | R | \(\pi\) |
| cot x | R – {n\(\pi\) : n \(\in\) I} | R | \(\pi\) |
| sec x | R – {(2n+1)\(\pi/2\); n \(\in\) I} | (-\(\infty\), -1] \(\cup\) [1, \(\infty\)] | \(2\pi\) |
| cosec x | R – {n\(\pi\) : n \(\in\) I} | (-\(\infty\), -1] \(\cup\) [1, \(\infty\)] | \(2\pi\) |
Trigonometric ratios of some standard angles :
(i) sin\(18^{\circ}\) = sin\(\pi\over 10\) = \(\sqrt{5}-1\over 4\) = cos\(72^{\circ}\) = cos\(2\pi\over 5\)
(ii) cos\(36^{\circ}\) = cos\(\pi\over 5\) = \(\sqrt{5}+1\over 4\) = sin\(54^{\circ}\) = sin\(3\pi\over 10\)
(iii) sin\(72^{\circ}\) = sin\(2\pi\over 5\) = \(\sqrt{10 + 2\sqrt{5}}\over 4\) = cos\(18^{\circ}\) = cos\(\pi\over 10\)
(iv) sin\(36^{\circ}\) = sin\(\pi\over 5\) = \(\sqrt{10 – 2\sqrt{5}}\over 4\) = cos\(54^{\circ}\) = cos\(3\pi\over 10\)
(v) sin\(15^{\circ}\) = sin\(\pi\over 12\) = \(\sqrt{3}-1\over {2\sqrt{2}}\) = cos\(75^{\circ}\) = cos\(5\pi\over 12\)
(vi) cos\(15^{\circ}\) = sin\(\pi\over 12\) = \(\sqrt{3}+1\over {2\sqrt{2}}\) = sin\(75^{\circ}\) = sin\(5\pi\over 12\)
(vii) tan\(15^{\circ}\) = tan\(\pi\over 12\) = \(2 – \sqrt{3}\) = \(\sqrt{3}-1\over {\sqrt{3}+1}\) = cot\(75^{\circ}\) = cot\(5\pi\over 12\)
(viii) tan\(75^{\circ}\) = tan\(5\pi\over 12\) = \(2 + \sqrt{3}\) = \(\sqrt{3}+1\over {\sqrt{3}-1}\) = cot\(15^{\circ}\) = cot\(\pi\over 12\)
(ix) tan(\(22.5^{\circ}\)) = tan\(\pi\over 8\) = \(\sqrt{2}-1\) = cot(\(67.5^{\circ}\)) = cot\(3\pi\over 8\)
(x) tan(\(67.5^{\circ}\)) = tan\(3\pi\over 8\) = \(\sqrt{2}+1\) = cot(\(22.5^{\circ}\)) = cot\(\pi\over 8\)
Example : Evaluate sin\(78^{\circ}\) – sin\(66^{\circ}\) – sin\(42^{\circ}\) + sin\(6^{\circ}\)
Solution : (sin\(78^{\circ}\) – sin\(66^{\circ}\)) – (sin\(42^{\circ}\) – sin\(6^{\circ}\)-)
= 2cos(\(60^{\circ}\))sin(\(18^{\circ}\)) – 2cos(\(36^{\circ}\))sin(\(30^{\circ}\))
= sin\(18^{\circ}\) – cos\(36^{\circ}\)
= (\(\sqrt{5}-1\over 4\)) – (\(\sqrt{5}+1\over 4\)) = \(-1\over 2\)
