What is the Value of Cos 45 Degrees ?

Solution :

The value of cos 45 degrees is $1\over \sqrt{2}$.

Proof :

Let ABC be a triangle, right angled at B, in which $\angle$ A = $\angle$ C = 45 degrees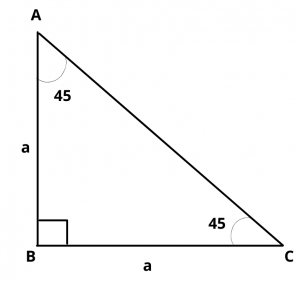

$\therefore$  BC = AB

Let  AB = BC = a

Then by pythagoras theorem,

$AC^2$ = $AB^2$ + $BC^2$ = $a^2$ + $a^2$ = $2a^2$

$\implies$  AC = $\sqrt{2}a$

In $\Delta$ ABC,  $\angle$ C = 45 degrees

By using trigonometric formulas,

$cos 45^{\circ}$ = $base\over hypotenuse$ = $b\over h$

$cos 45^{\circ}$  = side adjacent to 45 degrees/hypotenuse = $BC\over AC$ = $a\over \sqrt{2}a$ = $1\over \sqrt{2}$

Hence, the value of $cos 45^{\circ}$ = $1\over \sqrt{2}$