Solution :
The value of cos 30 degrees is \(\sqrt{3}\over 2\).
Proof :
Consider an equilateral triangle ABC with each side of length of 2a. Each angle of \(\Delta\) ABC is of 60 degrees. Let AD be the perpendicular from A on BC.
\(\therefore\) AD is the bisector of \(\angle\) A and D is the mid-point of BC.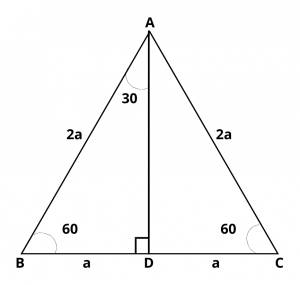
\(\therefore\) BD = DC = a and \(\angle\) BAD = 30 degrees.
In \(\Delta\) ADB, \(\angle\) D is a right angle, AB = 2a and BD = a
By Pythagoras theorem,
\(AB^2\) = \(AD^2\) + \(BD^2\) \(\implies\) \(2a^2\) = \(AD^2\) + \(a^2\)
\(\implies\) \(AD^2\) = \(4a^2\) – \(a^2\) = \(3a^2\) \(\implies\) AD = \(\sqrt{3}a\)
Now, In triangle ADB, \(\angle\) BAD = 30 degrees
By using trigonometric formulas,
\(cos 30^{\circ}\) = \(base\over hypotenuse\) = \(b\over h\)
\(cos 30^{\circ}\) = side adjacent to 30 degrees/hypotenuse = \(AD\over AB\) = \(\sqrt{3}\over 2a\) = \(\sqrt{3}\over 2\)
Hence, the value of \(cos 30^{\circ}\) = \(\sqrt{3}\over 2\)
