Here you will learn what is the point of inflection and properties of maxima and minima.
Let’s begin –
What is the Point of Inflection ?
A point of inflection is a point at which a curve is changing concave upward to concave downward, or vice versa.
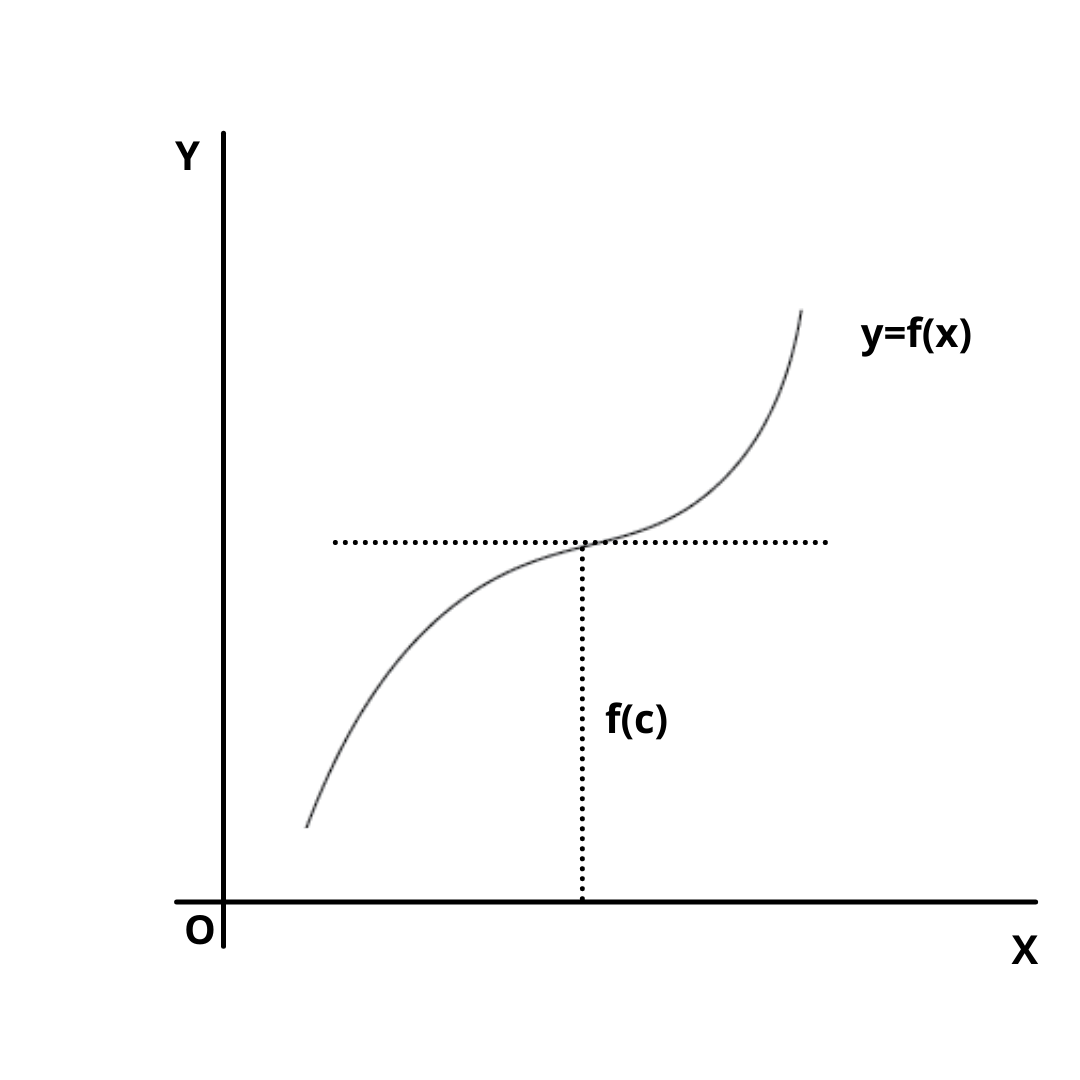
A curve y = f(x) has one of its points x = c as an inflection point, if
(i) f”(c) = 0 or is not defined and
(ii) f”(x) changes sign as x increases through x = c.
The later conditions may be replaced by f”'(c) \(\ne\) 0 when f”'(c) exists.
Thus, x = c is a point of inflection if f”(c) = 0 and f”'(c) \(\ne\) 0.
Example : The point of inflection for the curve f(x) =\(x^{5/3}\) is –
(A) (1, 1)
(B) (0, 0)
Solution : Here, f”(x) = \(10\over 9x^{1/3}\)
from the given points we find that (0, 0) is the point of the curve where
f”(x) does not exist but sign of f”(x) changes about this point.
Hence (0, 0) is the required point.
Properties of Maxima and Minima
(i) If f(x) is continous function in its domain, then atleast one maximum or one minimum must lie between two equal values of f(x).
(ii) Maxima and minima occur alternately, that is, between two maxima there is one minimum and vice-versa.
(iii) If f(x) \(\rightarrow\) \(\infty\) as x \(\rightarrow\) a or b and f'(x) = 0 only for one value of x (say c) between a and b, then f(c) is necessarily the minimum and the least value.
If f(x) \(\rightarrow\) -\(\infty\) as x \(\rightarrow\) a or b, then f(c) is necessarily the maximum and the greatest value.
Related Questions
Find the point of inflection for the curve y = \(x^3 – 6x^2 + 12x + 5\).
Find the inflexion point of f(x) = \(3x^4 – 4x^3\).
Find the point of inflexion for f(x) = \(x^4\over 12\) – \(5x^3\over 6\) + \(3x^2\) + 7.
