Prove that the line joining the mid-points of two sides of a triangle is parallel to the third side.

Solution :

Given : A triangle ABC in which D and E are mid point of sides AB and AC respectively.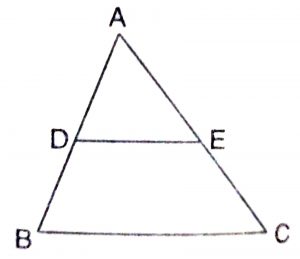

To Prove :  DE || BC

Proof : Since sides AB and AC have D and E as mid points,

\(\therefore\)   AD = DB  and  AE = EC

\(\implies\)  \(AD\over DB\) = 1  and  \(AE\over EC\) = 1

\(\implies\)  \(AD\over DB\) = \(AE\over EC\)

Hence, By converse of Basic proportionality theorem,

DE || BC.