Prove that the line drawn from the mid-point of one side of triangle parallel to another side bisects the third side.

Solution :

Given : A triangle ABC in which D is the mid point of side AB and the line DE is drawn parallel to BC, meeting AC in E.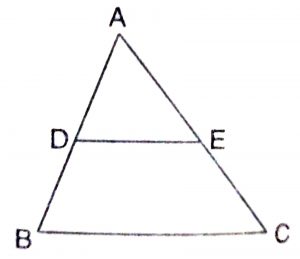

To Prove :  AE = EC

Proof : In triangle ABC, DE || BC

By basic proportionality theorem,

\(AD\over DB\) = \(AE\over EC\)                  ………..(1)

But given that D is the mid point of AB,

AB = DB     \(\implies\)   \(AD\over DB\) = 1             …….(2)

From (1) and (2), we obtain that

\(AE\over EC\) = 1          \(\implies\)   AE = EC.

Hence, E bisects AC.