Solution :
Given : ABC is a triangle and AD is the median.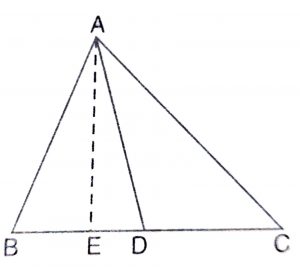
To Prove :
(i) \({AB}^2\) + \({AC}^2\) = 2[\({AD}^2\) + \({BD}^2\)]
(ii) \({AB}^2\) + \({AC}^2\) = 2\({AD}^2\) + 2\([{1\over 2}BC]^2\)
Construction : Draw AE \(\perp\) BC
Proof : In right angled triangle ABE, by Pythagoras theorem,
\({AB}^2\) = \({BE}^2\) + \({AE}^2\) ………(1)
In right angled triangle AEC, by Pythagoras theorem,
\({AC}^2\) = \({EC}^2\) + \({AE}^2\) ……….(2)
(i) Adding (1) and (2), we get
\({AB}^2\) + \({AC}^2\) = 2\({AE}^2\) + \({BE}^2\) + \({EC}^2\)
= 2\({AE}^2\) + \({(BD – ED)}^2\) + \({(DC + ED)}^2\)
= 2\({AE}^2\) + \({BD}^2\) + \({ED}^2\) + \({DC}^2\) + \({ED}^2\)
= 2(\({AE}^2\) + \({ED}^2\)) + \({BD}^2\) + \({DC}^2\)
Since in right triangle AED, \({AE}^2\) + \({ED}^2\) = \({AD}^2\) and BD = CD
= 2\({AD}^2\) + \({BD}^2\) + \({BD}^2\)
= 2[\({AD}^2\) + \({BD}^2\)]
(ii) Since AD is median,
\(\therefore\) BC = 2BD
\({AB}^2\) + \({AC}^2\) = 2\({AD}^2\) + 2\([{1\over 2}BC]^2\)
