Here you will learn what is onto function with definition and examples.
Let’s begin –
Onto Function (Surjection) Definition
Definition : A function f : A \(\rightarrow\) B is said to be an onto function if every element of B is the f-image of some element of A i.e. , if f(A) = B or range of f is the codomain of f.
Thus, f : A \(\rightarrow\) B is a surjection iff for each b \(\in\) B, there exist a \(\in\) A such that f(a) = b
Also Read : Types of Functions in Maths – Domain and Range
Example : Let g : X \(\rightarrow\) Y be the function represented by the following diagram :
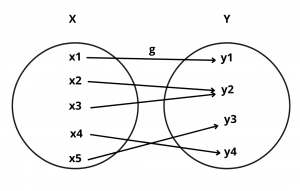
Solution : Under function g every element in Y has its pre-image X. So, g : X \(\rightarrow\) Y is onto.
Algorithm to Check for Onto
Let f : A \(\rightarrow\) B be the given function.
1). Choose an arbitrary element y in b.
2). Put f(x) = y
3). Solve the equation f(x) = y for x and obtain x in terms of y. Let x = g(y).
4). If for all values of y \(\in\) B, the values of x obtained from x = g(y) are in A, then f is onto.
Note : If range is same as codomain, then f is onto function.
Example : Let f : R \(\rightarrow\) R given by f(x) = \(x^3 + 2\) for all x \(\in\) R. Then, find whether it is onto or not.
Solution : Let y be the arbitrary element of R. Then,
f(x) = y \(\implies\) \(x^3 + 2\) = y \(\implies\) x = \((y – 2)^{1/3})\)
Clearly, for all y \(\in\) R, \((y – 2)^{1/3})\) is a real number. Thus, for all y \(\in\) R (co-domain) there exist x = \((y – 2)^{1/3})\) in R (domain) such that f(x) = \(x^3 + 2\) = y.
Hence, f : R \(\rightarrow\) R is an onto function.
