Here you will learn what is many one function with definition and examples.
Let’s begin –
Many One Function
Definition : A function f : A \(\rightarrow\) B is said to be a many-one function if two or more elements of set A have the same image in B.
Thus, f : A \(\rightarrow\) B is a many-one if there exist x, y \(\in\) A such that x \(\ne\) y but f(x) = f(y).
In other words, f : A \(\rightarrow\) B is a many-one if it is not a one-one function.
Also Read : Types of Functions in Maths – Domain and Range
Example : Let f : A \(\rightarrow\) B and g : X \(\rightarrow\) Y be two functions represented by the following diagrams :
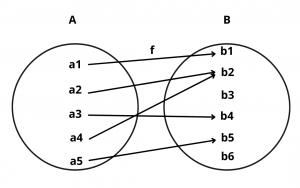
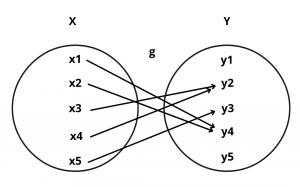
Solution : Clearly, a2 \(\ne\) a4 but f(a2) = f(a4) and x1 \(\ne\) x2 but g(x1) = g(x2). So, f and g are many-one.
Example : Let A = {-1, 1, -2, 2} and B = {1, 4, 9, 16}. Consider f : A \(\rightarrow\) B given by f(x) = \(x^2\).
Solution : Then, f(-1) = 1, f(1) = 1, f(-2) = 4 and f(2) = 4. Thus, 1 and -1 have the same image. Similarly, 2 and -2 also have the same image. So, f is many-one.