Here you will learn what is one one function with definition and examples.
Let’s begin –
One One Function Definition
Definition : A function f : A \(\rightarrow\) B is said to be a one-one function or an injection if different elements of A have different images in B.
Thus, f : A \(\rightarrow\) B is one-one
\(\iff\) a \(\ne\) b \(\implies\) f(a) \(\ne\) f(b) for all a, b \(\in\) A
\(\iff\) f(a) = f(b) \(\implies\) a = b for all a, b \(\in\) A
Also Read : Types of Functions in Maths – Domain and Range
Example : Let f : A \(\rightarrow\) B and g : X \(\rightarrow\) Y be two functions represented by the following diagrams :
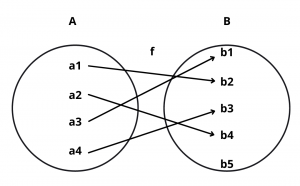
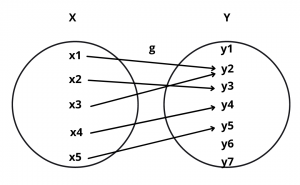
Solution : Clearly, f : A \(\rightarrow\) B is a one one function. But, g : X \(\rightarrow\) Y is not one-one because two different elements x1 and x3 have the same image under function g.
Example : Let A = {1, 2, 3, 4}, B = {1, 2, 3, 4, 5, 6} and f : A \(\rightarrow\) B be a function defined by f(x) = x + 2 for all x \(\in\) A.
Solution : We observe that f as a set of ordered pairs can be written as f = {(1, 3), (2, 4), (3, 5), (4, 6)}
Clearly, different elements in A have different images under function f.
So, f : A \(\rightarrow\) B is an injection or one-one.
Algorithm to Check for Injection
1). Take two arbitrary elements x, y (say) in the domain of f.
2). Put f(x) = f(y)
3). Solve f(x) = f(y). If it gives x = y only, then f : A \(\rightarrow\) B is a one-one function (or an injection) otherwise not.
Number of One One Function
If A and B are two sets having m and n elements respectively such that m \(\le\) n, then the total number of one-one functions from A to B is
\(^nC_m \times m!\)
where m! is m factorial.
