Question : On dividing \(x^3 – 3x^2 + x + 2\) by a polynomial g(x), the quotient and the remainder were x – 2 and -2x + 4, respectively. Find g(x).
p(x) = \(x^3 – 3x^2 + x + 2\)
q(x) = x – 2 and r(x) = -2x + 4
Solution : By division algorithm, we know that
p(x) = q(x) \(\times\) g(x) + r(x)
Therefore, \(x^3 – 3x^2 + x + 2\) = (x – 2) \(\times\) g(x) + (-2x + 4)
\(\implies\) \(x^3 – 3x^2 + x + 2 + 2x – 4\) = (x – 2) \(\times\) g(x)
\(\implies\) g(x) = \(x^3 – 3x^2 + 3x – 2\over x – 2\)
On dividing \(x^3 – 3x^2 + x + 2\) by x – 2, we get g(x)
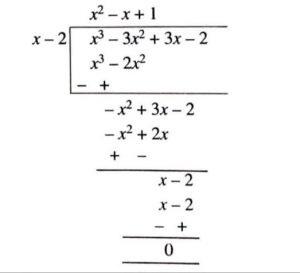
Hence, g(x) = \(x^2 – x + 1\).
