Solution :
Since two zeroes are \(\sqrt{5\over 3}\) and -\(\sqrt{5\over 3}\),
x = \(\sqrt{5\over 3}\) and x = -\(\sqrt{5\over 3}\)
\(\implies\) (x – \(\sqrt{5\over 3}\))(x + \(\sqrt{5\over 3}\)) = \(3x^2 – 5\) is a factor of the given polynomial. Now, we apply the division algorithm to the given polynomial and \(3x^2 – 5\).
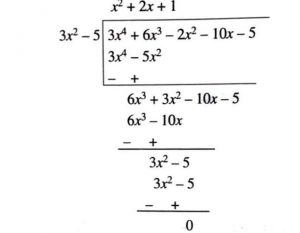
First term of quotient is \(3x^4\over 3x^2\) = \(x^2\)
Second term of quotient is \(6x^3\over 3x^2\) = 2x
Third term of the quotient is \(3x^2\over 3x^2\) = 1
So, \(3x^4 + 6x^3 – 2x^2 – 10x – 5\) = (\(3x^2 – 5\))(\(x^2 + 2x + 1\)) + 0 = (\(3x^2 – 5\))\({(x + 1)}^2\)
Quotient = \(x^2 + 2x + 1\) = \({(x + 1)}^2\)
Zeroes of \({(x + 1)}^2\) are -1 and -1.
Hence, all its zeroes are \(\sqrt{5\over 3}\), -\(\sqrt{5\over 3}\), -1, -1.
