Here you will learn normal form of a line equation with proof and examples.
Let’s begin –
Normal Form of a Line (Perpendicular form of line)
The equation of the straight line upon which the length of of the perpendicular from the origin is p and this perpendicular makes an angle \(\alpha\) with x-axis is
\(xcos\alpha\) + \(ysin\alpha\) = p.
Proof :
Let the line AB be such that the length of the perpendicular OQ from the origin O to the line be p and \(\angle\) XOQ = \(\alpha\)
Let P(x, y) be any point on the line. Draw PL \(\perp\) OX, LM \(\perp\) OQ and PN \(\perp\) LM. Then,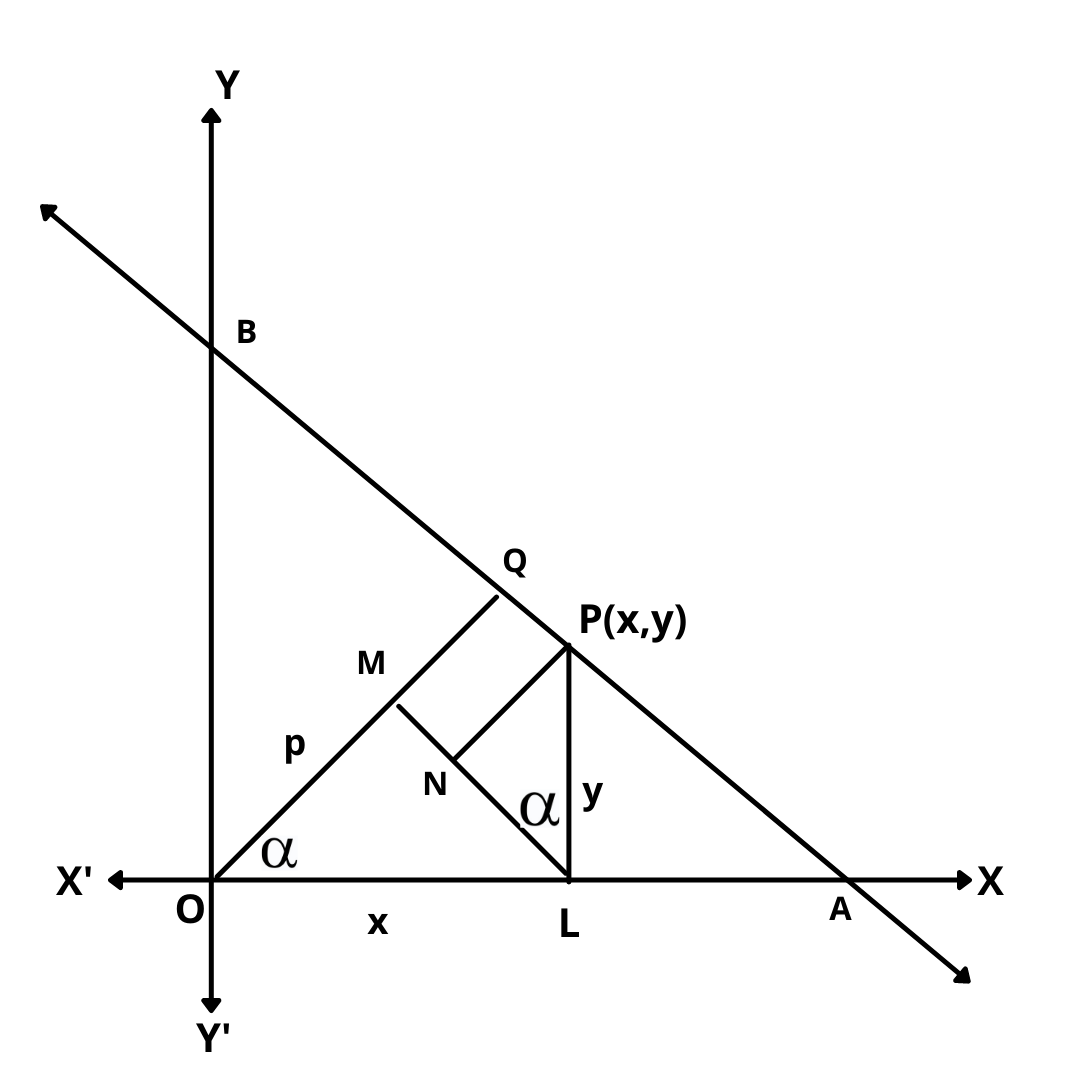
OL = x and LP = y
In triangle OLM, we have
\(cos\alpha\) = \(OM\over OL\)
\(\implies\) OM = OL \(cos\alpha\) = x \(cos\alpha\).
In triangle PNL, we have
\(sin\alpha\) = \(PN\over PL\)
\(\implies\) PN = PL \(sin\alpha\) = y \(sin\alpha\)
\(\implies\) MQ = PN = y \(sin\alpha\)
Now, p = OQ = OM + MQ = \(xcos\alpha\) + \(ysin\alpha\)
Hence, the equation of the required line is
\(xcos\alpha\) + \(ysin\alpha\) = p.
Example : Find the equation of the line which is at a distance 3 from the origin and the perpendicular from the origin to the line makes an angle of 30 with the positive direction of the x-axis.
Solution : Here, p = 3, \(\alpha\) = 30
Equation of the line in the normal form is
x cos 30 + y sin 30 = 3
\(\implies\) x \(\sqrt{3}\over 2\) + \(y\over 2\) = 3
\(\implies\) \(\sqrt{3}\) x + y = 6.
which is the required equation line.
