Here you will learn intercept form of a line equation i.e. intercept cut by line on x-axis and y-axis with examples.
Let’s begin –
Intercept Form of a Line
The equation of a line which cuts off intercepts a and b respectively from the x and y-axes is
\(x\over a\) + \(y\over b\) = 1.
Proof : Let AB be the line which cuts off intercepts OA = a and OB = b on the x and y axes respectively.
Let P(x,y) be any point on the line. Draw PL \(\perp\) OX.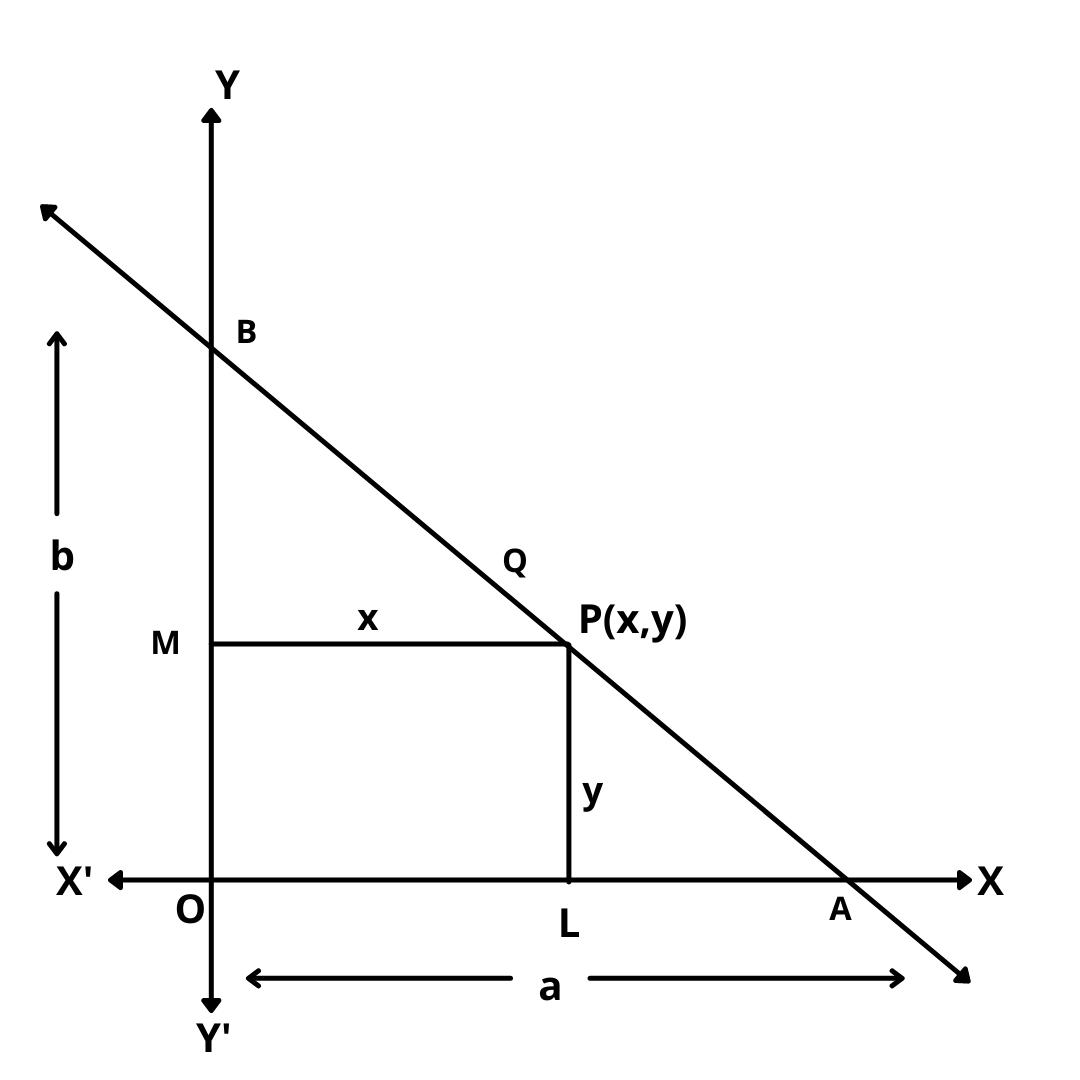
Then, OL = x and PL = y.
Clearly,
Area of OAB = Area of triangle OPA + Area of triangle OPB
\(1\over 2\) OA.OB = \(1\over 2\) OA.PL + \(1\over 2\) OB.PM
\(1\over 2\)ab = \(1\over 2\)ay + \(1\over 2\)bx
\(\implies\) ab = ay + ax
\(\implies\) \(x\over a\) + \(y\over b\) = 1.
This is the required equation of the line in the intercept form.
Example : Find the equation of the line which cut off an intercept 4 on the positive direction of x-axis and an intercept 3 on the negative direction of y-axis.
Solution : Here a = 4, b = -3.
So, the equation of the line is
\(x\over a\) + \(y\over b\) = 1 or, \(x\over 4\) + \(y\over -3\) = 1. or 3x – 4y = 12.
Example : Find the equation of the straight line which passes through the point (4, -2) and whose intercept on y-axis is twice that on X-axis.
Solution : let the equation of line be
\(x\over a\) + \(y\over b\) = 1 ………….(i)
It is given that its y-intercept is twice the x-intercept
\(\therefore\) b = 2a
Putting b = 2a in (i), we get
2x + y = 2a ………………..(ii)
It passes through point (4, -2).
\(\therefore\) 8 – 2 = 2a \(\implies\) a = 3.
Substituting a = 3 in (ii), we get
2x + y = 6 as the equation of the required line.