Here you will learn formula to find the length of latus rectum of parabola with examples.
Let’s begin –
Latus Rectum of Parabola
A double ordinate through the focus is called the latus rectum i.e. the latus rectum of a parabola is a chord passing through the focus perpendicular to the axis.
In the given figure, LSL’ is the latus rectum of the parabola \(y^2\) = 4ax.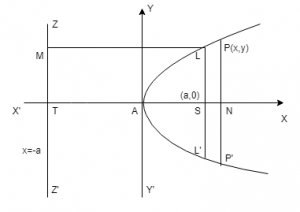
By the symmetry of the curve SL = SL’ = \(\lambda\) (say). So, the coordinates of L are \((a, \lambda)\).
Since L lies on \(y^2\) = 4ax, therefore
\({\lambda}^2\) = \(4a^2\) \(\implies\) \(\lambda\) = 2a
\(\implies\) LL’ = \(2\lambda\) = 4a
Hence, Latus Rectum = 4a
Note : The length of latus rectum of all other forms of parabola i.e. \(x^2\) = 4ay , \(y^2\) = -4ax and \(x^2\) = -4ay is also equal to 4a.
Also Read : Different Types of Parabola Equations
Coordinates of Latus Rectum
The coordinates of L and L’ , end points of the latus rectum, are (a, 2a) and (a, -2a) respectively.
Example : For the given parabola, find the length of the latus rectum:
(i) \(y^2\) = 8x
(ii) \(x^2\) = -16y
Solution :
(i) The given parabola is of the form \(y^2\) = 4ax, where 4a = 8 i.e. a = 2.
Hence, Length of latus rectum = 4a = 8
(ii) The given parabola is of the form \(x^2\) = -4ay, where 4a = 16 i.e. a = 4.
Hence, Length of latus rectum = 4a = 16
Example : Find the latus rectum of the parabola \(y^2 – 8y – x + 19\) = 0
Solution : The given equation is
\(y^2 – 8y – x + 19\) = 0 \(\implies\) \(y^2 – 8y\) = x – 19
\(\implies\) \(y^2 – 8y + 16\) = x – 19 + 16
\(\implies\) \((y – 4)^2\) = (x – 3)
The equation is of the form \(y^2\) = 4ax, where 4a = 1 i.e. a = 1/4.
Hence, Length of Latus Rectum is 4a = 1.
