Solution :
In triangle BCA,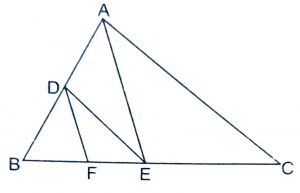
Given, DE || AC
By Basic proportionality theorem, we have
\(BE\over EC\) = \(BD\over DA\) ……..(1)
In triangle BEA,
Given, DF || AE
By Basic proportionality theorem, we have
\(BF\over FE\) = \(BD\over DA\) ……..(2)
From (1) and (2), we obtain that
\(BF\over FE\) = \(BE\over EC\)
