In the figure, DE || OQ and DF || OR. Show that EF || QR.

Solution :

In triangle PQO,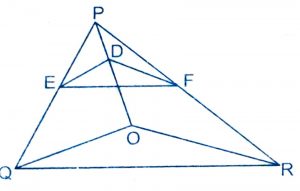

Given,        DE || OQ

By Basic proportionality theorem, we have

\(PE\over EQ\) = \(PD\over DO\)           ……..(1)

In triangle POR,

Given,        DF ||  OR

By Basic proportionality theorem, we have

\(PD\over DO\) = \(PF\over FR\)           ……..(2)

From (1) and (2), we obtain that

\(PE\over EQ\) = \(PF\over FR\)

Hence, By converse of basic proportionality theorem, we have

EF || QR