In the figure, ABD is triangle right angled at A and AC \(\perp\) BD. Show that (i) \({AB}^2\) = BC.BD (ii) \({AC}^2\) = BC.DC (iii) \({AD}^2\) = BD.CD

Solution :

(i) Since, AC \(\perp\) BD, therefore,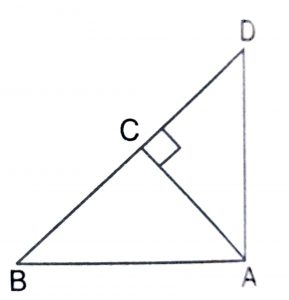

\(\triangle\) ABC ~ \(\triangle\) DBA  and  each triangle is similar to whole triangle ABD.

\(\implies\)  \(AB\over BD\) = \(BC\over AB\)

So, \({AB}^2\) = BC.BD

(ii) Since, \(\triangle\) ABC ~ \(\triangle\) DAC, therefore,

\(\implies\)  \(AC\over BC\) = \(DC\over AC\)

So, \({AC}^2\) = BC.DC

(iii) Since, \(\triangle\) ACD ~ \(\triangle\) BAD, therefore,

\(\implies\)  \(AD\over CD\) = \(BD\over AD\)

So, \({AD}^2\) = BD.CD