ABC is an isosceles triangle right angled at C. Prove that \({AB}^2\) = \(2{AC}^2\).

Solution :

Since ABC is an isosceles right triangle, right angled at C, therefore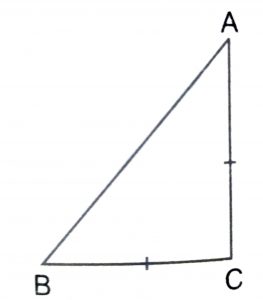

\({AB}^2\) = \({AC}^2\) + \({BC}^2\)

Since given that the triangle is isosceles,

\(\therefore\)  BC = AC

\(\implies\) \({AB}^2\) = \({AC}^2\) + \({AC}^2\)

So, \({AB}^2\) = \(2{AC}^2\)