In the figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that \(area(\triangle ABC)\over area(\triangle DBC)\) = \(AO\over DO\).

Solution :

Given : Two triangles ABC and DBC which stand on the same base BC but on the opposite sides of BC.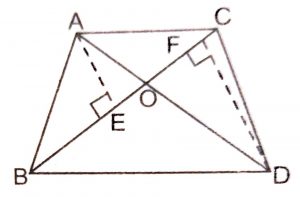

To Prove : \(area(\triangle ABC)\over area(\triangle DBC)\) = \(AO\over DO\)

Construction : Draw AE \(\perp\) BC and DF \(\perp\) BC.

Proof : In triangles AOE and DOF, we have :

\(\angle\) AEO = \(\angle\) DFO = 90

\(\angle\) AOE = \(\angle\) DOF       (vertically opposite angles)

By AA similarity, we have :

\(\triangle\) AOE ~ \(\triangle\) DOF

So, \(AE\over DF\) = \(AO\over OD\)            ……..(1)

Now, \(area(\triangle ABC)\over area(\triangle DBC)\) = \({1\over 2} \times BC \times AE\over {1\over 2}\times BC \times DF\) = \(AE\over DF\) = \(AO\over OD\)

\(\therefore\)     \(area(\triangle ABC)\over area(\triangle DBC)\) = \(AO\over OD\).