Diagonals of trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD, find the ratio of the areas of triangles AOB and COD.

Solution :

In triangles AOB and COD,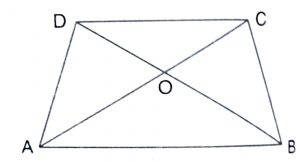

\(\angle\) AOB = \(\angle\) COD       (vertically opposite angles)

\(\angle\) OAB = \(\angle\) OCD        (corresponding angles)

\(\therefore\) By AA similarity,

\(\triangle\) AOB ~ \(\triangle\) COD

\(\implies\)  \(area(\triangle AOB)\over area(\triangle COD)\) = \({AB}^2\over {DC}^2\)

\(\implies\)  \(area(\triangle AOB)\over area(\triangle COD)\) = = \({2DC}^2\over {DC}^2\) = \(4\over 1\)

Hence, Area of triangle AOB : Area of triangle COD = 4 : 1