Equation of Ellipse in Standard Form

The equation of ellipse in standard form referred to its principal axes along the coordinate axes is

\(x^2\over a^2\) + \(y^2\over b^2\) = 1,

where a > b & \(b^2\) = \(a^2(1 – e^2)\) \(\implies\) \(a^2\) – \(b^2\) = \(a^2e^2\).

where e = eccentricity (0 < e < 1)

Foci : S = (ae, 0) & S’ = (-ae, 0)

Vertices : A’ = (-a, 0) and A’ = (a, 0)

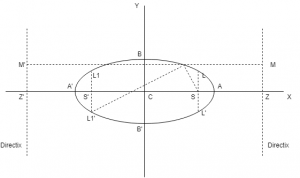
(a) Equation of directrix of Ellipse :

x = \(a\over e\) and x = \(-a\over e\)

(b) Major axis of Ellipse :

The line segment A’A in which the foci S’ & S lie is of length 2a & is called the major axis (a > b) of the ellipse. The Point of intersection of major axis with directrix is called the foot of the directrix(z).

(c) Minor axis of Ellipse :

The y-axis intersects the ellipse in the points B’ = (0,-b) & B = (0,b). The line segment B’B of length 2b (b < a) is called the minor axis of the ellipse.

Both the axes minor and major together are called Principal Axes of the ellipse.

(d) Double ordinate of Ellipse :

A chord perpendicular to major axis is called double ordinate of ellipse.

(e) Latus Rectum of Ellipse :

The focal chord perpendicular to major axis is called the latus rectum of ellipse.

(i) Length of latus rectum(LL’) = \(2b^2\over a\) = \({(minor axis)}^2\over {major axis}\) = 2a(1 – \(e^2\))

(ii) Equation of latus rectum : x = \(\pm\)ae

(iii) Ends of latus rectum are L(ae, \(b^2\over a\)), L'(ae, -\(b^2\over a\)), L1(-ae, \(b^2\over a\)),
L1′(-ae, -\(b^2\over a\))

(f) Eccentricity of Ellipse :

e = \(\sqrt{1 – {b^2\over a^2}}\)

Example : Find the equation of ellipse in standard form having center at (1, 2), one focus at (6, 2) and passing through the point (4, 6).

Solution : With center at (1, 2), the equation of the ellipse is \((x – 1)^2\over a^2\) + \((y – 2)^2\over b^2\) = 1. It passes through the point (4, 6)

\(\implies\) \(9\over a^2\) + \(16\over b^2\) = 1 …..(i)

Distance between focus and center = (6 – 1) = 5 = ae

\(\implies\) \(b^2\) = \(a^2\) – \(a^2e^2\) = \(a^2\) – 25 …..(ii)

Solving (i) and (ii)

we get \(a^2\) = 45 and \(b^2\) = 20

Hence, the equation of the ellipse is \((x – 1)^2\over 45\) + \((y – 2)^2\over 20\) = 1

Equation of Ellipse in Standard Form