Here, you will learn different types of ellipse and their basic definitions with their graphs.
Let’s begin –
Different Types of Ellipse
(a) First type of Ellipse is
\(x^2\over a^2\) + \(y^2\over b^2\) = 1, where a > b
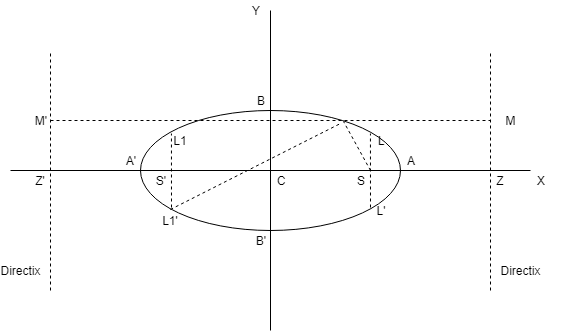
(a) AA’ = Major axis = 2a
(b) BB’ = Minor axis = 2b
(c) Vertices = (\(\pm a\), 0)
(d) Latus rectum LL’ = L1L1′ = \(2a^2\over b\), equation x = \(\pm\)ae
(e) Ends of latus rectum are : L(ae, \(b^2\over a\)), L'(ae, -\(b^2\over a\)), L1(-ae, \(b^2\over a\)), L1′(-ae, -\(b^2\over a\))
(f) Equation of directrix y = \(\pm a\over e\)
(g) Eccentricity : e = \(\sqrt{1 – {b^2\over a^2}}\)
(h) Foci : S = (ae, 0) & S’ = (-ae, 0)
(b) Second type of Ellipse is
\(x^2\over a^2\) + \(y^2\over b^2\) = 1 (a < b)
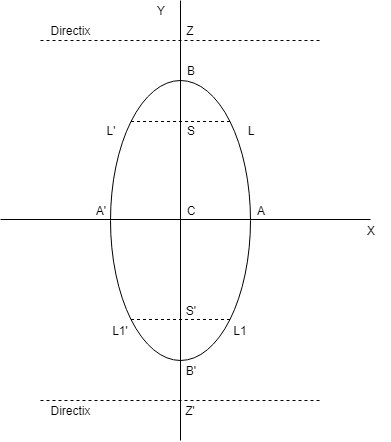
(a) AA’ = Minor axis = 2a
(b) BB’ = Major axis = 2b
(c) Vertices = (0, \(\pm b\))
(d) Latus rectum LL’ = L1L1′ = \(2a^2\over b\), equation y = \(\pm\)be
(e) Ends of latus rectum are : L(\(a^2\over b\), be), L'(-\(a^2\over b\), be), L1(\(a^2\over b\), -be), L1′(-\(a^2\over b\), -be)
(f) Equation of directrix y = \(\pm b\over e\)
(g) Eccentricity : e = \(\sqrt{1 – {a^2\over b^2}}\)
(h) Foci : S = (0, be) & S’ = (0, -be)
Line and an ellipse
The line y = mx + c meets the ellipse \({x_1}^2\over a^2\) + \({y_1}^2\over b^2\) = 1 in two real, coincident, or imaginary according as \(c^2\) is < = or > \(a^2m^2 + b^2\).
Hence y = mx + c is tangent to the ellipse \({x_1}^2\over a^2\) + \({y_1}^2\over b^2\) = 1 if \(c^2\) = \(a^2m^2 + b^2\)
Related Questions
The foci of an ellipse are \((\pm 2, 0)\) and its eccentricity is 1/2, find its equation.
