Question :
E and F are points on the side PQ and PR respectively of a triangle PQR. For each of the following cases state whether EF || QR :
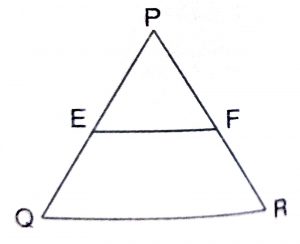
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Solution :
By converse of basic proportionality theorem or Thales theorem that if a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
(i) Here, \(PE\over EQ\) = \(3.9\over 3\) = \(1.3\over 1\)
\(PF\over FR\) = \(3.6\over 2.4\) = \(3\over 2\) = 1.5
Thus, \(PE\over EQ\) \(\ne\) \(PF\over FR\)
No, EF is not parallel to QR.
(ii) Here, \(PE\over EQ\) = \(4\over 4.5\)
\(PF\over FR\) = \(8\over 9\) = \(4\over 4.5\)
Thus, \(PE\over EQ\) = \(PF\over FR\)
Yes, EF is parallel to QR.
(iii) Here, \(PQ\over PE\) = \(1.28\over 0.18\)
\(PR\over PF\) = \(2.56\over 0.36\) = \(1.28\over 0.18\)
Thus, \(PQ\over PE\) \(\ne\) \(PR\over PF\)
Yes, EF is parallel to QR.
