Here you will learn how to find argument or amplitude of a complex number with examples.
Let’s begin –
Amplitude of a Complex Number (Argument of Complex Number)
Let z = x + iy, Then,
The angle \(\theta\) which OP makes with the positive direction of x-axis in anticlockwise sense is called the argument or amplitude of complex number z.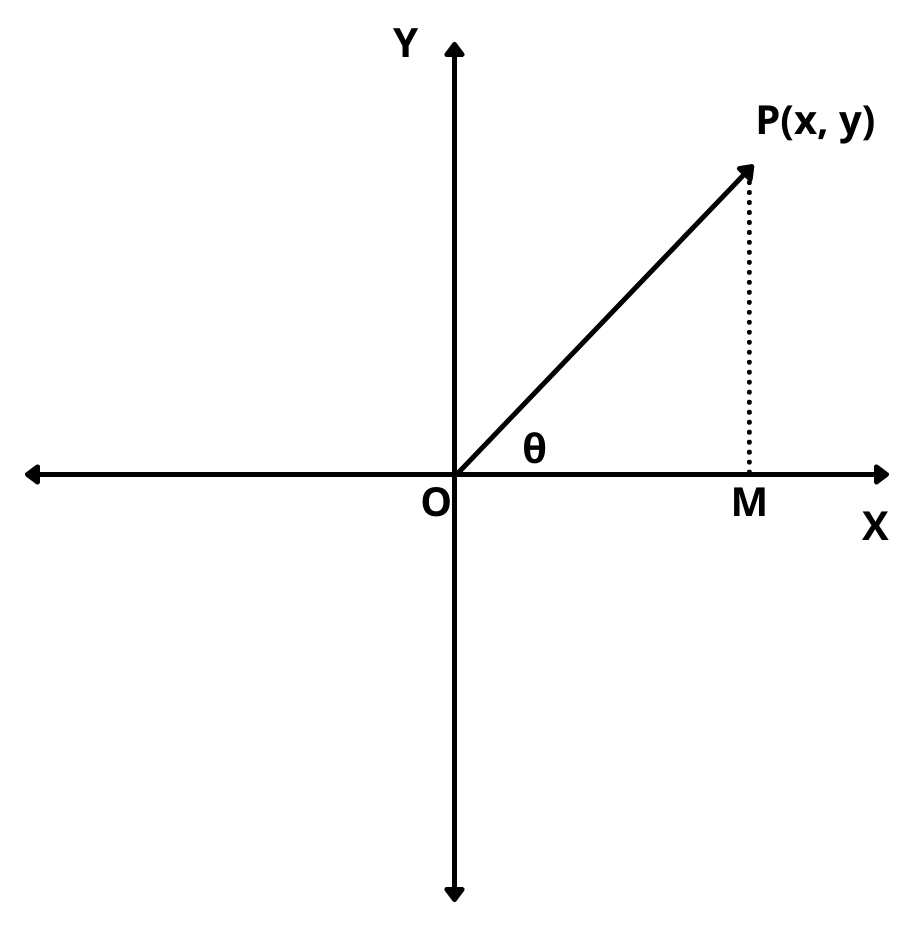
It is denoted by arg(z) or amp(z).
From Figure, we have
\(tan\theta\) = \(PM\over OM\) = \(y\over x\) = \(Im (z)\over Re (z)\)
\(\implies\) \(\theta\) = \(tan^{-1}({y\over x}\))
This angle \(\theta\) has infinitely many values differing by multiples of \(2\pi\). The unique value of \(\theta\) such that -\(\pi\) < \(\theta\) \(\le\) \(\pi\) is called the principal value of the amplitude or principal argument.
In order to find the argument of a complex number z = x + iy for different quadrants, we use the following algorithm.
Algorithm :
1). Find the value of \(tan^{-1}| y/x |\) lying between 0 and \(\pi/2\). Let it be \(\alpha\).
2). Determine in which quadrant the point P(x, y) belongs.
(i) If P(x, y ) belongs to the first quadrant, then arg(z) = \(\alpha\).
(ii) If P(x, y ) belongs to the second quadrant, then arg(z) = \(\pi – \alpha\).
(iii) If P(x, y ) belongs to the third quadrant, then arg(z) = -(\(\pi – \alpha\)) or \(\pi + \alpha\).
(iv) If P(x, y ) belongs to the fourth quadrant, then arg(z) = -\(\alpha\) or \(2\pi – \alpha\).
Example : Find the argument of the following complex numbers.
(i) \(1 + i\sqrt{3}\)
(ii) \(-2 + 2i\sqrt{3}\)
(iii) \(-\sqrt{3} – i\)
(iv) \(2\sqrt{3} – 2i\)
Solution :
(i) Let z = \(1 + i\sqrt{3}\) and let \(\alpha\) be the acute angle given by
\(\alpha\) = \(tan^{-1}|{Im(z)\over Re(z)}|\) = \(tan^{-1}|{\sqrt{3}\over 1}|\)
\(\implies\) \(\alpha\) = \(\pi\over 3\)
Since, Re(z) > 0 and Im(z) > 0. So, it lies in first quadrant
\(\therefore\) arg(z) = \(\alpha\) = \(\pi\over 3\)
(ii) Let z = \(-2 + 2i\sqrt{3}\) and let \(\alpha\) be the acute angle given by
\(\alpha\) = \(tan^{-1}|{Im(z)\over Re(z)}|\) = \(tan^{-1}|{2\sqrt{3}\over -2}|\)
\(\implies\) arg(z) = \(\alpha\) = \(\pi\over 3\)
Since, Re(z) < 0 and Im(z) > 0. So, it lies in second quadrant
\(\therefore\) arg(z) = \(\pi – \alpha\) = \(\pi\) – \(\pi\over 3\) = \(2\pi\over 3\)
(iii) Let z = \(-\sqrt{3} – i\) and let \(\alpha\) be the acute angle given by
\(\alpha\) = \(tan^{-1}|{Im(z)\over Re(z)}|\) = \(tan^{-1}|{-1\over -\sqrt{3}}|\)
\(\implies\) \(\alpha\) = \(\pi\over 6\)
Since, Re(z) < 0 and Im(z) < 0. So, it lies in third quadrant
\(\therefore\) arg(z) = -(\(\pi – \alpha\)) = -(\(\pi\) – \(\pi\over 6\)) = \(-5\pi\over 6\)
(iv) Let z = \(2\sqrt{3} – 2i\) and let \(\alpha\) be the acute angle given by
\(\alpha\) = \(tan^{-1}|{Im(z)\over Re(z)}|\) = \(tan^{-1}|{-2\over 2\sqrt{3}}|\)
\(\implies\) \(\alpha\) = \(\pi\over 6\)
Since, Re(z) > 0 and Im(z) < 0. So, it lies in fourth quadrant
\(\therefore\) arg(z) = -\(\alpha\) = -\(\pi\over 6\)
