Here you will learn what is the polar form of complex numbers with examples.
Let’s begin –
Polar Form of Complex Numbers
Let z = x + iy be a complex number represented by a point P(x, y) in the argand plane.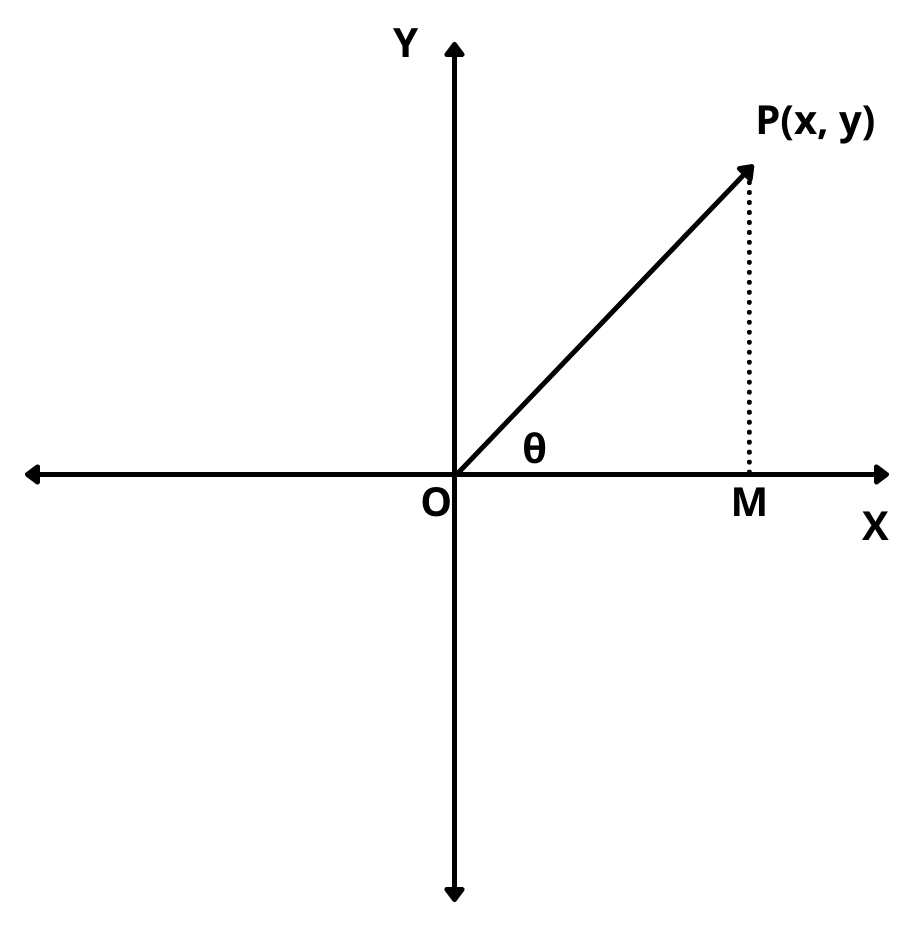
Then by the geometrical representation of z = x + iy, we have
OP = | z | and angle POX = \(\theta\) = arg (z)
In triangle POM, we have
\(cos\theta\) = \(OM\over OP\) = \(x\over | z |\) \(\implies\) x = | z | \(cos\theta\)
and, \(sin\theta\) = \(PM\over OP\) = \(y\over | z |\) \(\implies\) x = | z | \(sin\theta\)
So, z = x + iy
z = | z | \(cos\theta\) + i | z | \(sin\theta\)
\(\implies\) z = | z | \((cos\theta + i sin\theta)\)
\(\implies\) z = r\((cos\theta + i sin\theta)\), where r = | z | and \(\theta\) = arg (z)
This form of z is called a polar form of z. If we use the general value of the argument of \(\theta\), then the polar form of z is given by
z = r\((cos(2n\pi + \theta) + i sin(2n\pi + \theta))\), where r = | z | and \(\theta\) = arg (z) and n is an integer.
Example : Write the following complex numbers in the polar form :
(i) \(-3\sqrt{2} + 3\sqrt{2}i\)
(ii) 1 + i
Solution :
(i) Let z = \(-3\sqrt{2} + 3\sqrt{2}i\). Then,
r = | z | = \(\sqrt{(-3\sqrt{2})^2 + (3\sqrt{2})^2}\) = 6
Let \(tan\alpha\) = |\(Im(z)\over Re(z)\)| = 1 \(\implies\) \(\alpha\) = \(\pi\over 4\)
Since the point representing z lies in the second quadrant. Therefore, the argument of z is given by
\(\theta\) = \(\pi – \alpha\) = \(\pi\) – \(\pi\over 4\) = \(3\pi\over 4\).
So, the polar form of z is
z = r\((cos\theta + i sin\theta)\) = 6\(cos{3\pi\over 4} + isin{3\pi\over 4}\)
(ii) Let z = 1 + i. Then,
r = | z | = \(\sqrt{1^2 + 1^2}\) = \(\sqrt{2}\)
Let \(tan\alpha\) = |\(Im(z)\over Re(z)\)| = 1 \(\implies\) \(\alpha\) = \(\pi\over 4\)
Since the point (1, 1) representing z lies in the first quadrant. Therefore, the argument of z is given by
\(\theta\) = \(\alpha\) = \(\pi\over 4\)
So, the polar form of z is
z = r\((cos\theta + i sin\theta)\) = \(\sqrt{2}\)\(cos{\pi\over 4} + isin{\pi\over 4}\)