Solution :
The general solution of \(tan \theta\) = 0 is given by \(\theta\) = \(n\pi\), n \(\in\) Z.
Proof :
We have,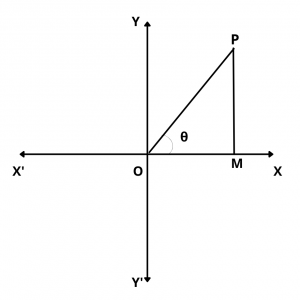
\(tan \theta\) = \(PM\over OM\)
\(\therefore\) \(tan \theta\) = 0
\(\implies\) \(PM\over OM\) = 0
\(\implies\) PM = 0
\(\implies\) OP coincides with OX or OX’
\(\implies\) \(\theta\) = 0, \(\pi\), \(2\pi\), ….., \(-\pi\), \(-2\pi\), \(-3\pi\), ….
\(\implies\) \(\theta\) = \(n\pi\), n \(\in\) Z
Hence, \(\theta\) = \(n\pi\), n \(\in\) Z is the general solution of \(tan \theta\) = 0.
