Here you will learn what is slope intercept form of a line with examples.
Let’s begin –
What is Slope Intercept Form of a Line ?
The equation of a line with slope m and making an intercept on y-axis is
y = mx + c
Proof :
Let the given line intersects y-axis at Q and makes an angle \(\theta\) with x-axis.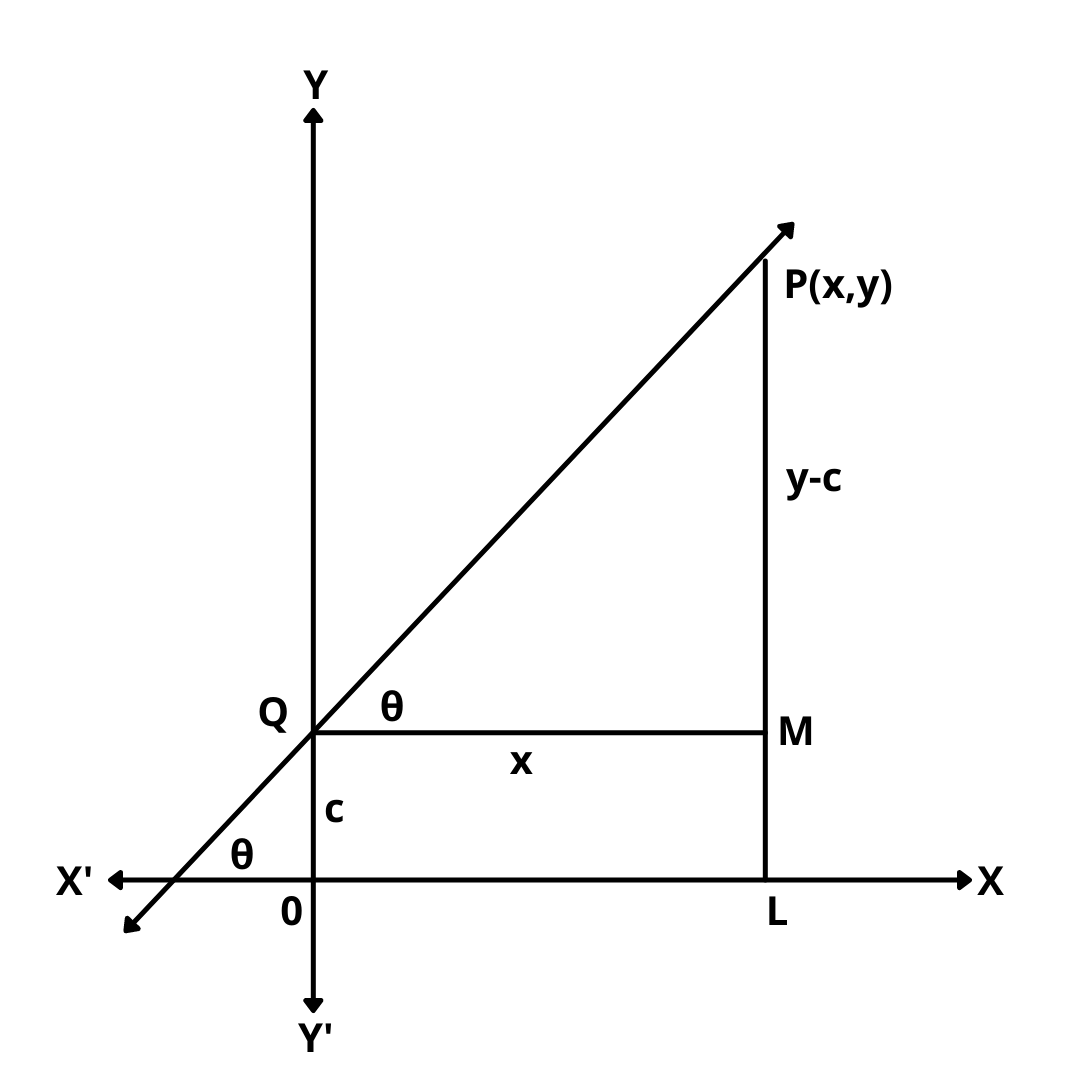 
Then, m = \(tan\theta\).
Let P(x, y) be any point on the line. Draw PL perpendicular to x-axis and QM \(\perp\) PL.
Clearly, \(\angle\) MPQ = \(\theta\), QM = OL = x
and, PM = PL – ML = PL – OQ = y – c
From triangle PMQ, we have
\(\tan\theta\) = \(PM\over QM\) = \(y – c\over x\)
\(\implies\) m = \(y – c\over x\)
\(\implies\) y = mx + c
which is the required equation of the line.
Remark 1 :
If the line passes through the origin, the 0 = m0 + c \(\implies\) c = 0. Therefore, the equation of a line passing through origin is y = mx, where m is the slope of the line.
Remark 2 :
If the line is parallel to x-axis, then m = 0, therefore the equation of a line parallel to x-axis is y = c.
Example : Find the equation of a line with slope -1 and cutting off an intercept of 4 units on negative direction of y-axis.
Solution : Here m = -1 and c = -4
Substituting these values in y = mx + c, we obtain that the equation of the line is
y = – x – 4 or, x + y + 4 = 0
Example : Find the equation of a straight line which cut off an intercept of 5 units on negative direction of y-axis and makes an angle of 120 with the positive direction of x-axis.
Solution : Here m = tan 120 = tan(90 + 30) = -cot 30 = -\(\sqrt{3}\) and c = -5
Substituting these values in y = mx + c, we obtain that the equation of the line is
y = – \(\sqrt{3}\)x – 5
or, \(\sqrt{3}\)x + y + 5 = 0