Here, you will learn vector quantities and scalar quantities and mathematical description of vector and scalar.
Let’s begin –
Vectors constitute one of the several Mathematical systems which can be usefully employed to provide mathematical handling for certain types of problems in Geometry, Mechanics and other branches of Applied Mathematics.
Vectors facilitate mathematical study of such physical quantities as possess Direction in addition to Magnitude. Velocity of a particle, for example, is one such quantity.
Physical quantities are broadly divided in two categories viz (a) Vector Quantities & (b) Scalar quantities.
Vector Quantities
Any quantity, such as velocity, momentum, or force, that has both magnitude and direction and for which vector addition is defined and meaningful; is treated as vector quantities.
Note :
Quantities having magnitude and direction but not obeying the vector law of addition will not be treated as vectors.
For example, the rotations of a rigid body through finite angles have both magnitude & direction but do not satisfy the law of vector addition therefore not a vector.
Scalar Quantities
A quantity, such as mass, length, time, density or energy, that has size or magnitude but does not involve the concept of direction is called scalar quantity.
Mathematical Description of Vector & Scalar
To understand vectors mathematically we will first understand directed line segment.
Directed line Segment :
Any given portion of a given straight line where the two end points are distinguished as Initial and Terminal is called a Directed Line Segment.
The directed line segment with initial point A and terminal point B is denoted by the symbol AB. The two end points of a directed line segment are not interchangeable and the directed line segments.
\(\overrightarrow{AB}\) and \(\overrightarrow{BA}\) must be thought of as different.
(a) Vector :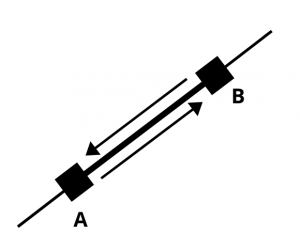 A directed line segment is called vector. Every directed line segment have three essential characteristics.
A directed line segment is called vector. Every directed line segment have three essential characteristics.
(i) Length : The length of AB will be denoted by the symbol |AB|
Clearly, we have |AB| = |BA|
(ii) Support : The line of unlimited length of which a directed line segment is a part is called its line of support or simply the Support.
(iii) Sense : The sense of AB is from A to B and that of BA from B to A so that the sense of a directed line segment is from its initial to the terminal point.
(b) Scalar : Any real number is a scalar.
Equality of Two Vectors
Two vectors are said to be equal if they have.
(a) the same length,
(b) the same or parallel supports and
(c) the same sense.
