Types of Discontinuities – Removable and Nonremovable

Discontinuity :

The function f(x) will be discontinuous at x = a in either of the following situations and it has the following types of discontinuities discusses below :

1. \(\displaystyle{\lim_{x \to a^-}}\) f(x) and \(\displaystyle{\lim_{x \to a^+}}\) f(x) exist but are not equal.

2. \(\displaystyle{\lim_{x \to a^-}}\) f(x) and \(\displaystyle{\lim_{x \to a^+}}\) exist and are equal but not equal to f(a).

3. f(a) is not defined.

4. At least one of the limits between LHL and RHL does not exist.

Types of Discontinuities :

1). Removable types of discontinuities :

In this case \(\displaystyle{\lim_{x \to {a}}}\) f(x) exists but it is not equal to f(a) then the function is said to have removable discontinuity or discontinuity of the first kind. So, In this case we can redefine function such that \(\displaystyle{\lim_{x \to a}}\) f(x) = f(a) & make it continuous at x = a. Removable type of discontinuity can be further classified as :

(a) Missing point discontinuity :

Where \(\displaystyle{\lim_{x \to a}}\) f(x) exists but f(a) is not defined.

(b) Isolated point discontinuity :

Where \(\displaystyle{\lim_{x \to a}}\) f(x) exists and f(a) also exists but \(\displaystyle{\lim_{x \to a}}\) f(x) \(\ne\) f(a).

Example : Examine the function f(x) = \(\begin{cases} x-1, & x < 0 \\ {1\over 4}, & x = 0 \\ {x^2-1} , & x > 0 \end{cases}\)

Solution : from the given function, \(\displaystyle{\lim_{x \to 0^-}}\) f(x) = \(\displaystyle{\lim_{x \to 0^+}}\) f(x) = -1, but f(0) = \(1\over 4\)

Thus, f(x) has isolated type removable discontinuity and f(x) could be made continuous by taking f(0) = -1

\(\implies\) f(x) = \(\begin{cases} x-1, & x < 0 \\ {-1}, & x = 0 \\ {x^2-1} , & x > 0 \end{cases}\)

2). Non-Removable types of discontinuities :

In this case \(\displaystyle{\lim_{x \to {a}}}\) f(x) does not exist, then it is not possible to make the function continuous by redefining it. Such a discontinuity is called as non-removable discontinuity or discontinuity of 2nd kind. Non-removable type of discontinuity can be further classified as :

(a) Finite type discontinuity :

In such type of discontinuity left hand limit and right hand limit at a point exists but are not equal.

(b) Infinite type discontinuity :

In this type of discontinuity atleast one of limit viz. LHL and RHL tends to infinity.

(c) Oscillatory type discontinuity :

e.g. f(x) = \(sin{\pi\over x}\) at x = 0; f(x) has a non-removable oscillatory type discontinuity at x = 0.

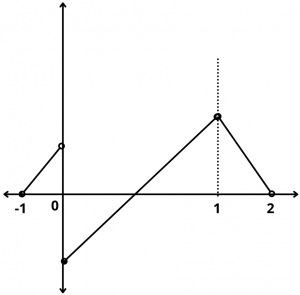
Example : From the given graph note that

(i) f is continuous at x = -1.

(ii) It has isolated discontinuity at x = 1.

(iii) It has missing point discontinuity at x = 2.

(iv) It has non-removable (finite type) discontinuity at origin.