Here, you will learn state polygon law of vector addition, subtraction of vectors and multiplication of vector by scalars.
Let’s begin –
Polygon law of vector Addition (Addition of more than two vectors)
Addition of more than two vectors is found to be by repetition of triangle law.
Suppose we have to find the sum of five vectors \(\vec{a}\), \(\vec{b}\), \(\vec{c}\), \(\vec{d}\) and \(\vec{e}\). If these vectors be represented by line segment \(\overrightarrow{OA}\), \(\overrightarrow{AB}\), \(\overrightarrow{BC}\), \(\overrightarrow{CD}\) and \(\overrightarrow{DE}\) respectively, then their sum will be denoted by \(\overrightarrow{OE}\). Thís is the vector represented by rest (last) side of the polygon OABCDE in reverse order. We can also make it clear this way :
By triangle’s law
i.e. \(\overrightarrow{OA}\) + \(\overrightarrow{AB}\) = \(\overrightarrow{OB}\) \(\implies\) \(\vec{a}\) + \(\vec{b}\) = \(\overrightarrow{OB}\)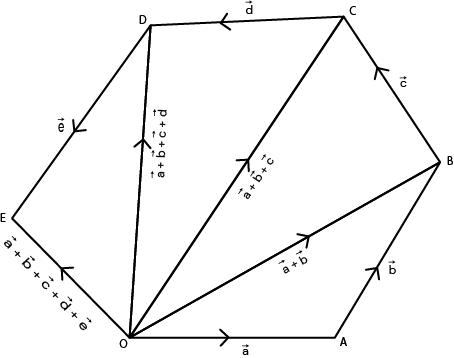
\(\overrightarrow{OB}\) + \(\vec{c}\) = \(\overrightarrow{OC}\) \(\implies\) (\(\vec{a}\) + \(\vec{b}\)) = \(\overrightarrow{OC}\)
\(\overrightarrow{OC}\) + \(\vec{d}\) = \(\overrightarrow{OD}\) \(\implies\) (\(\vec{a}\) + \(\vec{b}\) + \(\vec{c}\)) +\(\vec{d}\) = \(\overrightarrow{OD}\)
i.e. \(\overrightarrow{OD}\) + \(\vec{e}\) = \(\overrightarrow{OE}\) \(\implies\) (\(\vec{a}\) + \(\vec{b}\) +\(\vec{c}\) + \(\vec{d}\)) + \(\vec{e}\) = \(\overrightarrow{OE}\)
Here, we see that \(\overrightarrow{OE}\) isrepresented by the line segment joining the initial point O of the first vector \(\vec{a}\) and the final point of the last vector \(\vec{e}\).
In order to find the sum of more that two vectors by this method, a polygon is formed. Therefore this method is known as the polygon law of addition.
Subtraction of Vectors
Vector -\(\vec{b}\) has length equals to vector b but its direction is opposite. Subtraction of vector \(\vec{a}\) and \(\vec{b}\) is defined as addition of \(\vec{a}\) and (-\(\vec{b}\)). It is written as follows :
\(\vec{a}\) – \(\vec{b}\) = \(\vec{a}\) + (-\(\vec{b}\))
Multiplication of vector by scalars
If \(\vec{a}\) is a vector & m is a scalar, then m(\(\vec{a}\)) is a vector parallel to \(\vec{a}\) whose modulus is |m| times that of \(\vec{a}\). This multiplication is called SCALAR MULTIPLICATION. If \(\vec{a}\) & \(\vec{b}\) are vectors & m, n are scalars, then :
(1) m(\(\vec{a}\)) = (\(\vec{a}\))m = m(\(\vec{a}\))
(2) m(n\(\vec{a}\)) = n(m\(\vec{a}\)) = (mn)\(\vec{a}\)
(3) (m + n)\(\vec{a}\) = m\(\vec{a}\) + m\(\vec{a}\)
(4) m(\(\vec{a}\) + \(\vec{b}\)) = m\(\vec{a}\) + m\(\vec{b}\)
Hope you learnt state polygon law of vector addition, subtraction of vectors and multiplication of vector by scalars. To learn more practice more question and get ahead in competition. Good Luck!
