Here you will learn what is square root function with definition, graph, domain and range.
Let’s begin –
Square Root Function
The function that associates a real number x to +\(\sqrt{x}\) is called square root function. Since \(\sqrt{x}\) is real for x \(ge\) 0. So, we defined the square root function as follows :
Definition : The function f : \(R^+\) \(\rightarrow\) R defined by f(x) = +\(\sqrt{x}\) is called the square root function.
Also Read : Types of Functions in Maths – Domain and Range
Square Root Function Graph
The values of f(x) = +\(\sqrt{x}\) increase with the increase in x.
So, the graph of f(x) = +\(\sqrt{x}\) is :
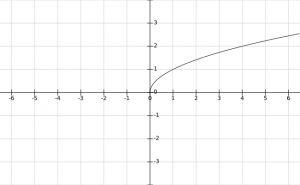
Domain and Range :
Clearly, the domain of the square root function is \(R^+\) i.e [\(0, \infty\)) and its range is also [\(0, \infty\)).
Domain : [\(0, \infty\))
Range : [\(0, \infty\))
