Here you will learn what is smallest integer function definition, graph and its domain and range with examples.
Let’s begin –
Smallest Integer Function (Ceiling Function)
Definition : For any real number x, we use the symbol \(\lceil x \rceil\) to denote the smallest integer greater than or equal to x.
For example, \(\lceil 4.7 \rceil\) = 5, \(\lceil -7.2 \rceil\) = -7, \(\lceil 5 \rceil\) = 5, \(\lceil 0.75 \rceil\) = 1 etc.
The function f : R \(\rightarrow\) R defined by f(x) = \(\lceil x \rceil\) for all x \(\in\) R is callled the smallest integer function or the ceiling function.
It is also a step function.
Also Read : Types of Functions in Maths – Domain and Range
Graph of Ceiling Function
The graph of the smallest integer function is given below.
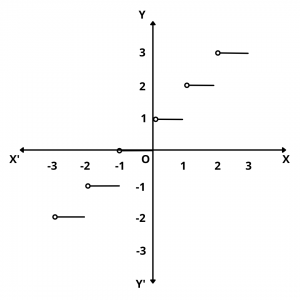
Domain and Range of Smallest Integer Function
We observe that the domain of the smallest integer function is the set R of all real numbers and its range is the set Z of all integers.
Domain : R
Range : Z
Properties :
Following are some properties of smallest integer function.
(i) \(\lceil -n \rceil\) = – \(\lceil n \rceil\) where n \(\in\) Z.
(ii) \(\lceil -x \rceil\) = – \(\lceil x \rceil\) + 1, where x \(\in\) R – Z
(iii) \(\lceil x + n \rceil\) = \(\lceil x \rceil\) + n, where x \(\in\) R – Z and n \(\in\) Z
(iv) \(\lceil x \rceil\) + \(\lceil -x \rceil\) = {1, if x \(\notin\) Z and 0, if x \(\in\) Z}
(v) \(\lceil x \rceil\) + \(\lceil -x \rceil\) = {2\(\lceil x \rceil\) – 1, if x \(\notin\) Z and 2\(\lceil x \rceil\), if x \(\in\) Z}.
