Here you will learn what is the formula to find the equation of radical axis of two circles.
Let’s begin –
Radical Axis of Two Circles
Definition : The locus of a point, which moves in such a way that the length of tangents drawn from it to the circle are equal and is called the radical axis.
If two circles are –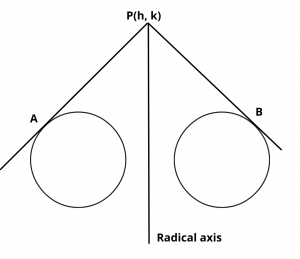
\(S_1\) = \(x^2 + y^2 + 2g_1x + 2f_1y + c_1\) = 0
\(S_2\) = \(x^2 + y^2 + 2g_2x + 2f_2y + c_2\) = 0
Let P(h, k) is a point and PA, PB are length of two tangents on the circles from point P,
Then from definition –
\(\sqrt{h^2 + k^2 + 2g_1h + 2f_1k + c_1}\) = \(\sqrt{h^2 + k^2 + 2g_2h + 2f_2k + c_2}\)
\(\implies\) \(2(g_1 – g_2)h + 2(f_1 – f_2)k + c_1 – c_2\) = 0
\(\therefore\) Locus of (h, k)
\(2x(g_1 – g_2)\) + \(2y(f_1 – f_2)\) + \(c1 – c_2\) = 0
\(S_1 – S_2\) = 0
which is the equation of radical axis.
Also Read : Pole and Polar of a Circle Equation
Radical Centre
The radical centre of three circles is the point from which length of tangents on three circles are equal i.e the point of intersection of radical axis of the circles is the radical centre of the circles.
To get the radical axis of three circle \(S_1\) = 0, \(S_2\) = 0, \(S_3\) = 0 we have to solve any two
\(S_1 – S_2\) = 0, \(S_2 – S_3\) = 0, \(S_3 – S_1\) = 0
