Here, you will learn one one and onto function (bijection) with definition and examples.
Let’s begin –
What is Bijection Function (One-One Onto Function) ?
Definition : A function f : A \(\rightarrow\) B is a bijection if it is one-one as well as onto.
In other words, a function f : A \(\rightarrow\) B is a bijection, if it is
(i) one-one i.e. f(x) = f(y) \(\implies\) x = y for all x, y \(\in\) A.
(ii) onto i.e. for all y \(\in\) B, there exist x \(\in\) A such that f(x) = y.
Also Read : Types of Functions in Maths – Domain and Range
Example : Let f : A \(\rightarrow\) B be a function represented by the following diagram :
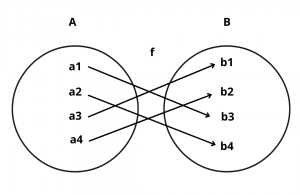
Solution : Clearly, f is a bijection since it is both one-one (injective) and onto (surjective).
Example : Prove that the function f : Q \(\rightarrow\) Q given by f(x) = 2x – 3 for all x \(\in\) Q is a bijection.
Solution : We observe the following properties of f.
One-One (Injective) : Let x, y be two arbitrary elements in Q. Then,
f(x) = f(y) \(\implies\) 2x – 3 = 2y – 3 \(\implies\) 2x = 2y \(\implies\) x = y
Thus, f(x) = f(y) \(\implies\) x = y for all x, y \(\in\) Q.
So, f is one-one.
Onto (Surjective) : Let y be an arbitrary element of Q. Then,
f(x) = y \(\implies\) 2x – 3 = y \(\implies\) x = \(y + 3\over 2\)
Clearly, for all y \(\in\) Q, x = \(y + 3\over 2\) \(\in\) Q. Thus, for all y \(\in\) Q (co-domain) there exist x \(\in\) Q (domain) given by x = \(y + 3\over 2\) such that f(x) = f(\(y + 3\over 2\)) = 2(\(y + 3\over 2\)) – 3 = y. That is every element in the co-domain has its pre-image in x.
So, f is onto function.
Hence, f : Q \(\rightarrow\) Q is a bijection.
Example : Let f : R \(\rightarrow\) R be a function defined as f(x) = \(2x^3 + 6x^2\) + 12x +3cosx – 4sinx; then f is-
Solution : We have f(x) = \(2x^3 – 6x^2\) + 12x + 3cosx – 4sinx
\(\implies\) f'(x) = \(6x^2 – 12x\) + 12 – 3sinx – 4cosx
\(\implies\) \(6x^2 – 12x\) + 12 = 6(\(x-1)^2\) + 6 = g(x) and 3sinx + 4cosx = h(x)
range of g(x) = [6, \(\infty\))
range of h(x) = [-5, 5]
hence f'(x) always lies in the interval [1, \(\infty\))
\(\implies\) f'(x) > 0
Hence f(x) is increasing i.e. one-one
Now x \(\rightarrow\) \(\infty\) \(\implies\) f \(\rightarrow\) \(\infty\) & x \(\rightarrow\) -\(\infty\) \(\implies\) f \(\rightarrow\) -\(\infty\) & f(x) is continous.
hence its range is R \(\implies\) f is onto so f is bijective.
Note :
(i) If a line parallel to x-axis cuts the graph of the functions atmost at one point, then the f is one-one.
(ii) If any line parallel to x-axis cuts the graph of the functions atleast at two points, then f is many-one.
(iii) If continous functions f(x) is always increasing or decreasing in whole domain, then f(x) is one-one.
(iv) All linear functions are one-one.
(v) All trigonometric functions in their domain are many one.
(vi) All even degree polynomials are many one.
(vii) Linear by linear is one-one.
(viii) Quadratic by quadratic with no common factor is many one.
(ix) A polynomial function of degree even define from R \(\rightarrow\) R will always be into.
(x) A polynomial function of degree odd defined from R \(\rightarrow\) R will always be onto
(xi) Quadratic by quadratic without any common factor define from R \(\rightarrow\) R is always an into function.
Thus a function can be of these four types :
(i) one-one onto (Injective and Surjective)(Also known as Bijective mapping)
(ii) one-one into (Injective but not surjective)
(iii) many-one onto (surjective but not injective)
(iv) many-one into (neither surjective nor injective)
