Formula for Circumference of Circle (Perimeter) – Examples

Here you will learn what is the formula for circumference of circle (perimeter of circle) with examples.

Let’s begin –

What is Circumference ?

The perimeter (boundary) of a circle is called its circumference. It is the distance covered by travelling once around circle.

Formula for Circumference of Circle (Perimeter of Circle)

Circumference of circle = $2\pi r$ 

where r is the radius of circle.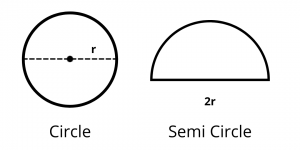

And $\pi$ is an irrational number whose approximate value is $22\over 7$ or 3.1415….. unless specified, the value of $\pi$ should be taken as $22\over 7$

Circumference (Perimeter) of Semicircle

Perimeter of Semicircle = $\pi r$ + 2r = $r(\pi + 2)$

Rotating Wheels

(i) Distance moved by a wheel in 1 rotation = circumference of the wheel

(ii) Number of rotations in 1 minute = distance moved in 1 minute/circumference.

Example : Find the circumference of the wheel of cycle’s whose diameter is 21 cm.

Solution : We have, Diameter = 21 cm 

$\implies$   Radius = $21\over 2$  = 10.5 cm

Circumference = $2\pi r$  = $2 \times {22\over 7} \times 10.5$ = 66 cm

Hence, the circumference of wheel of cycle is 66 cm

Example : If the diameter of a semi-circular plot is 14 m, then find its perimeter.

Solution : A semi-circle has been drawn with AB = 14 m as diameter.

$\therefore$  Its radius,     r = $d\over 2$ = $14\over 2$ = 7 m

$\therefore$   Perimeter of semi-circle of radius 7 m = $\pi r$ + 2r  = ${22\over 7} \times 7$ + $2\times 7$ = 36 m

Hence, the required perimeter is 36 m.