Here you will learn first derivative test for maxima and minima with examples.
Let’s begin –
First Derivative Test for Maxima and Minima
If f'(x) = 0 at a point (say x = a) and
(i) If f'(x) changes sign from positive to negative in the neighbourhood of x = a then x = a is said to be a point local maxima.
(ii) If f'(x) changes sign from negative to positive in the neighbourhood of x = a then x = a is said to be a point local minima.
Note – If f'(x) does not change sign i.e. has the same sign in a certain complete neighbourhood of a, then f(x) is either increasing or decreasing throughout this neighbourhood implying that x = a is not a point of extremum of f.
Example : Let f(x) = x + \(1\over x\) ; x \(\ne\) 0. Discuss the local maximum and local minimum values of f(x)
Solution : Here f'(x) = 1 – \(1\over x^2\) = \(x^2 – 1\over x^2\)
= \((x – 1)(x + 1)\over x^2\)
Using local number line rule, 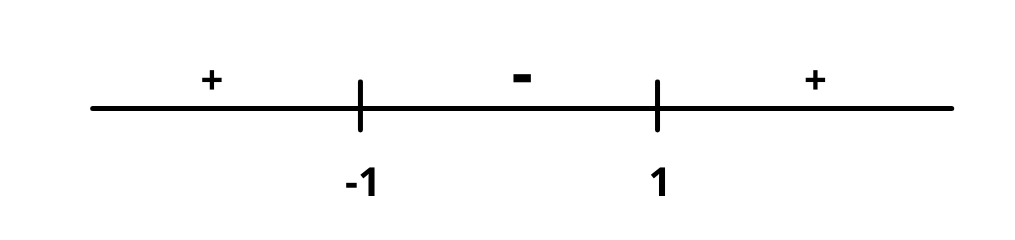
f(x) will have local maximum at x = – 1 and local minimum at x =1
\(\therefore\) local maximum value of f(x) = -2 at x = -1
and local minimum value of f(x) = 2 at x = 1
Example : Let f(x) = \(x^3 – 3x\). Discuss the local maximum and local minimum values of f(x)
Solution : Here f'(x) = \(3x^2 -3\) = 3(x + 1)(x – 1)
Using local number line rule, 
f(x) will have local maximum at x = – 1 and local minimum at x =1
\(\therefore\) local maximum value of f(x) = 2 at x = -1
and local minimum value of f(x) = -2 at x = 1
