Here you will learn what is conjugate hyperbola, equation of conjugate hyperbola and basic definitions of like eccentricity and latus rectum.
Let’s begin –
What is Conjugate Hyperbola ?
The hyperbola whose transverse & conjugate axes are respectively the conjugate and transverse axes of given hyperbola is called the conjugate hyperbola of given hyperbola.
The equation of the conjugate hyperbola of the hyperbola \(x^2\over a^2\) – \(y^2\over b^2\) = 1 is
-\(x^2\over a^2\) + \(y^2\over b^2\) = 1.
The graph of the conjugate hyperbola is shown in figure.
The eccentricity of the conjugate hyperbola is given by \(a^2\) = \(b^2(e^2-1)\) and the length of latus rectum is \(2a^2\over b\).
Conjugate Hyperbola & Basic Definitions :
The equation of the conjugate hyperbola is -\(x^2\over a^2\) + \(y^2\over b^2\) = 1.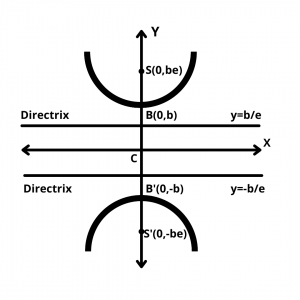
(a) Centre (0,0).
(b) Vertices (0,b) & (0,-b)
(c) foci \((0, \pm ae)\)
(d) Length of transverse axis is 2b
(e) Length of conjugate axis is 2a
(f) Equation of directrices is x = \(\pm {b\over e}\)
(g) Eccentricity is given by \(a^2\) = \(b^2(e^2-1)\)
(h) Length of latus rectum is \(2a^2\over b\).
(i) Equation of the transverse axis is x = 0.
(j) Equation of the conjugate axis is y = 0.
Example : Find the eccentricity of the conjugate hyperbola to the hyperbola \(x^2 – 3y^2\) = 1.
Solution : Equation of the conjugate hyperbola to the hyperbola \(x^2 – 3y^2\) = 1 is \(-x^2 + 3y^2\) = 1
\(\implies\) -\(x^2\over 1\) + \(y^2\over 1/3\) = 1.
Here \(a^2\) = 1, \(b^2\) = 1/3
Therefore eccentricity is e = \(\sqrt{1 + a^2/b^2}\) = 2.
Hope you learnt conjugate hyperbola, learn more concepts of hyperbola and practice more questions to get ahead in the competition. Good luck!
