Here you will learn what is the congruence of triangle and criteria for congruence of triangles i.e. SSS, SAS, ASA, AAS and RHS.
Let’s Begin –
Congruence of Triangles
Two triangles are congruent if the sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle. They are of the same shape and size. There are many criteria of congruence in triangles which are given below. We use this symbol (≅) to represent congruency of triangles.
Note :
(i) In congruent triangles corresponding parts are equal and we write in short ‘CPCT’ for corresponding parts of congruent triangles.
(ii) If two triangles are congruent then their perimeters and areas are equal.
Criteria For Congruence of Triangles
(i) SAS congruence rule of triangles
SAS stands for side angle side. In this Criterion, Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle.
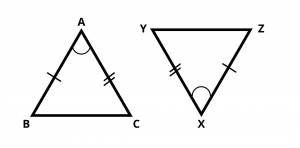
For given two triangles, AB = XZ , \(\angle\) A = \(\angle\) X and AC = XY, then using SAS rule, \(\Delta\) ABC ≅ \(\Delta\) XYZ.
(ii) ASA congruence rule
ASA stands for angle side angle. In this Criterion, Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of other triangle.
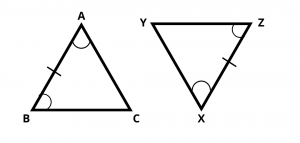
For given two triangles, AB = XZ , \(\angle\) A = \(\angle\) X and \(\angle\) B = \(\angle\) Z, then using ASA rule, \(\Delta\) ABC ≅ \(\Delta\) XYZ.
(iii) AAS Congruence Rule
AAS stands for angle angle side. In this Criterion, two triangles are congruent if any two pairs of angles and one pair of corresponding sides are equal.
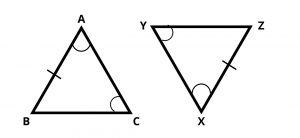
For given two triangles, \(\angle\) A = \(\angle\) X and \(\angle\) C = \(\angle\) Y, AB = XZ , then using AAS rule, \(\Delta\) ABC ≅ \(\Delta\) XYZ.
(iv) SSS congruence rule
SSS stands for side side side. In this Criterion, If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
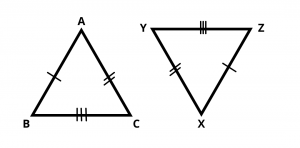
For given two triangles, AB = XZ , AC = XY and BC = YZ, then using SSS rule, \(\Delta\) ABC ≅ \(\Delta\) XYZ.
(v) RHS congruence rule (For Right Angle Triangle)
If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
Note that here RHS stands for Right angle – Hypotenuse – Side.
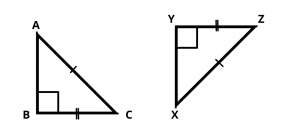
For given two right angle triangles, hypotenuse AC = hypotenuse XZ , BC = YZ and \(\angle\) B = \(\angle\) Y, then using RHS rule, \(\Delta\) ABC ≅ \(\Delta\) XYZ.
