Here you will learn what is the complement of a set definition with venn diagram and examples.
Let’s begin –
Complement of a Set
Definition : Let U be the universal set and let A be a set such that A \(\subset\) U. Then, the complement of A with respect to U is denoted by A’ or \(A^c\) or U – A and is defined the set of all those elements of U which are not in A.
Thus, A’ = {x \(\in\) U : x \(\notin\) A}
Clearly, x \(\in\) A’ \(\iff\) x \(\in\) A.
Venn Diagram :
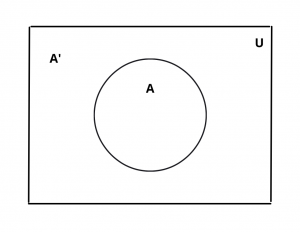
Also Read : Formulas and Operation of Sets
Example 1 : Let the set of natural numbers N = {1, 2, 3, 4, ….. } be the universal set and let A = {2, 4, 6, 8, ….}. Then A’ = {1, 3, 5, ….}/
Example 2 : If U = {1, 2, 3, 4, 5, 6, 7, 8, 9} and A = {1, 3, 5, 7, 9}, then A’ = {2, 4, 6, 8}.
Following results are direct consequence of the definition of the complement of a set.
(i) U’ = {x \(\in\) U : x \(\notin\) U} = \(\phi\)
(ii) \({\phi}’\) = {x \(\in\) U : x \(\notin\) \(\phi\)} = U
(iii) (A’)’ = {x \(\in\) U : x \(\notin\) A’} = {x \(\in\) U : x \(\in\) A} = A
(iv) A \(\cup\) A’ = U
(v) A \(\cap\) A’ = \(\phi\)
