Here you will learn common tangent to two circles i.e direct and transverse common tangents to two circles.
Let’s begin –
Common Tangent to Two Circles
Let two circles having centers \(C_1\) and \(C_2\) and radii, \(r_1\) and \(r_2\) and \(C_1\)\(C_2\) is the distance between their centres then :
(a) Both circles will touch :
(i) Externally : if \(C_1\)\(C_2\) = \(r_1\)\(r_2\) i.e, the distance between their centres is equal to sum of their radii and point P & T divides \(C_1\)\(C_2\) in the ratio \(r_1\) : \(r_2\) (internally & externally respectively). In this case there are three common tangents.
(ii) Internally : if \(C_1\)\(C_2\) = |\(r_1\) – \(r_2\)| i.e, the distance between their centres is equal to difference between their radii and point P divides \(C_1\)\(C_2\) in the ratio \(r_1\) : \(r_2\) externally and in this case there will be only <b>one common tangent.
(b) The circles will intersect :
when |\(r_1\) – \(r_2\)| < \(C_1\)\(C_2\) < \(r_1\) + \(r_2\) in this case there are two common tangent.
(c) The circles will not intersect :
(i) One Circle will lie inside the other circle if \(C_1\)\(C_2\) < |\(r_1\) – \(r_2\)| In this case there will be no common tangent.
(ii) When circle are apart from each other then \(C_1\)\(C_2\) > \(r_1\) + \(r_2\) and in this case there will be four common tangents.
Direct and Transverse Common Tangents
Let two circles having centers C1 and C2 and radii, r1 and r2 and C1C2 is the distance between their centres.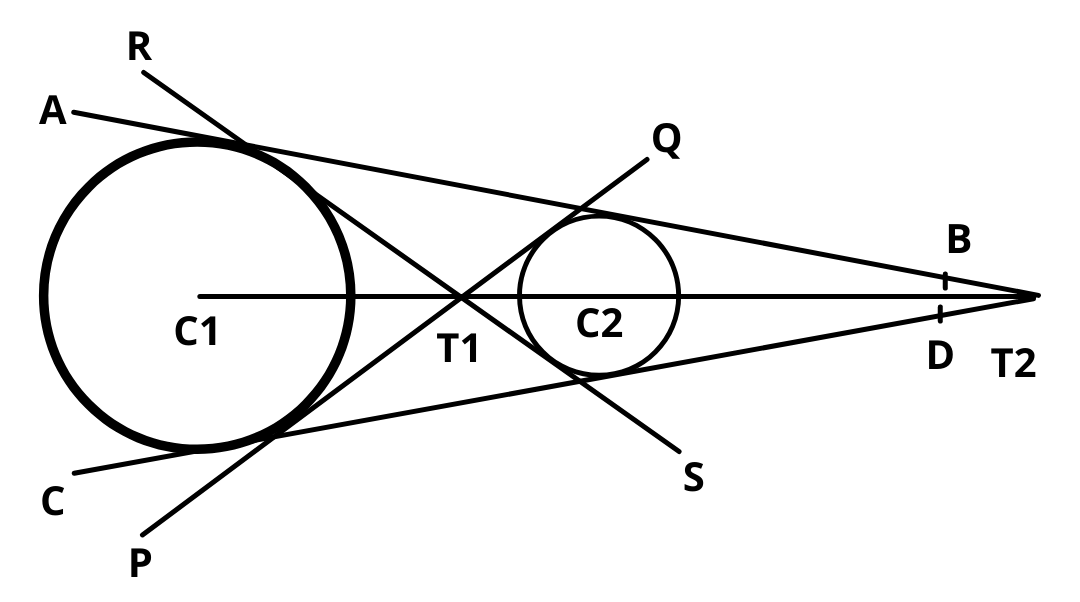
Lines PQ and Rs are called transverse or indirect or internal common tangents and these lines meet line C1C2 on T1 and T2 divide the line C1C2 in the ratio r1 : r2 internally and lines AB & CD are called direct or external common tangents. These lines meet C1C2 produced on T2. Thus T2 divides C1C2 externally in the ratio r1 : r2.
Length of Direct Common Tangent
Length = \(\sqrt{(C1C2)^2 – (r1 – r2)^2}\)
Length of Transverse Common Tangent
Length = \(\sqrt{(C1C2)^2 – (r1 + r2)^2}\)
Example : Find the number of common tangents to the circles \(x^2 + y^2\) = 1 and \(x^2 + y^2 – 2x – 6y + 6\) = 0
Solution : Let \(C_1\) be the center of circle \(x^2 + y^2\) = 1 i.e. \(C_1\) = (0, 0)
And \(C_2\) be the center of circle \(x^2 + y^2 – 2x – 6y + 6\) = 0 i.e. \(C_2\) = (1, 3)
Let \(r_1\) be the radius of first circle and \(r_2\) be the radius of second circle.
Then, \(r_1\) = 1 and \(r_2\) = 2
Learn how to find center and radius of circle here.
Now, \(C_1C_2\) = \(\sqrt{9 + 1}\) = \(\sqrt{10}\) and \(r_1 + r_2\) = 3
Since, \(C_1C_2\) > \(r_1 + r_2\)
Hence, there are four common tangents.
