Here you will learn equation of chord of contact of circle and length of chord of contact of circle.
Let’s begin –
Equation of Chord of Contact
A line joining the two points of contacts of two tangents drawn from a point outside the circle, is called chord of contact of that point.
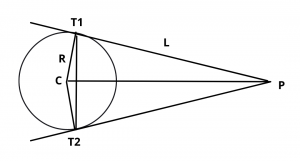
If two tangents \(PT_1\) and \(PT_2\) are drawn from the point P\((x_1, y_1)\) to the circle S = \(x^2 + y^2 + 2gx + 2fy + c\) = 0,
then the equation of the chord of contact \(T_1T_2\) is :
\(xx_1 + yy_1 + g(x + x_1) + f(y + y_1) + c\) = 0
i.e. T = 0 same as equation of tangent
Also Read : Length of Tangent to a Circle Formula From an External Point
Length and Angle Formula :
The formula for length is \(T_1T_2\) = \(2LR\over \sqrt{R^2 + L^2}\).
The formula for Angle between the pair of tangents from P\((x_1, y_1)\) = \(tan^{-1}({2RL\over L^2 – R^2})\).
Area of the Triangle Formed by Pair of Tangents Formula
The area of the triangle formed by the pair of the tangents and its chord of contact is given by the formula
\(RL^3\over R^2 + L^2\)
Where R is the radius of the circle and L is the length of the tangent from \((x_1, y_1)\) on S = 0.
