Solution :
We know that the sum of opposite angles of cyclic quadrilateral is 180 degrees.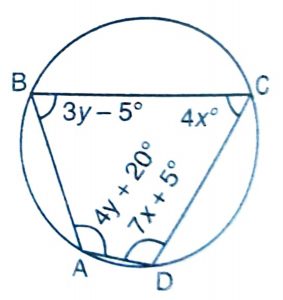
Angles A and C, Angles B and D form pairs of opposite angles in the given cyclic quadrilateral ABCD.
\(\angle\)A + \(\angle\)C = 180 and \(\angle\)B + \(\angle\)D = 180
\(\implies\) (4y + 20) + 4x = 180 and (3y – 5) + (7x + 5) = 180
\(\implies\) 4x + 4y – 160 = 0 \(\implies\) x + y – 40 = 0 …………(1)
and 7x + 3y – 180 = 0 …………(2)
Multiplying equation (1) by and subtracting from equation (2), we get
4x – 60 = 0 \(\implies\) x = 15
Put the value of x = 15 in equation (1), we get
15 + y – 40 = 0 \(\implies\) y = 25
Hence, \(\angle\)A = 4y + 20 = 120 degrees
\(\angle\)B = 3y – 5 = 70 degrees
\(\angle\)C = 4x = 60 degrees
\(\angle\)D = 7x + 5 = 110 degrees
