Here, you will learn triangle law of addition of vectors and parallelogram law of addition of vectors and properties of vector addition.
Let’s begin –
Addition of Vectors
The vectors have magnitude as well as direction, therefore their addition is different than addition of real numbers.
Let \(\vec{a}\) and \(\vec{b}\) be two vectors in a plane, which are represented by AB and CD. Their addition can be performed in the following two ways :
Triangle Law of Addition of Vectors
If two vectors can be represented in magnitude and direction by the two sides of a triangle, taken in order, then their sum will be represented by the third side in reverse order.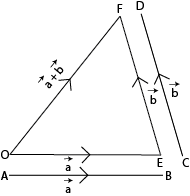
Let O be the fixed point in the plane of vectors. Draw a line segment \(\overrightarrow{OE}\) from O, equal and parallel to \(\overrightarrow{AB}\), which represents the vector \(\vec{a}\). Now from E, draw a line segment \(\overrightarrow{EF}\) equal and parallel to \(\overrightarrow{CD}\), which represents the vector \(\vec{b}\). Line segment \(\overrightarrow{OF}\) obtained by joining O and F represents the sum of vectors \(\vec{a}\) and \(\vec{b}\).
i.e. \(\overrightarrow{OE}\) + \(\overrightarrow{EF}\) = \(\overrightarrow{OF}\)
or \(\vec{a}\) + \(\vec{b}\) = \(\overrightarrow{OF}\)
This method of addition of two vectors is called Triangle law of addition of vectors.
Parallelogram Law of Addition of Vectors
If two vectors be represented in magnitude and direction by the two adjacent sides of a parallelogram then their sum will be represented by the diagonal through the co-initial point.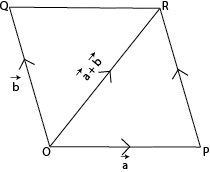
Let \(\vec{a}\) and \(\vec{b}\) be vectors drawn from point O denoted by line segments \(\overrightarrow{OP}\) and \(\overrightarrow{OQ}\). Now complete the parallelogram OPRQ. Then the vector represented by the diagonal OR will represent the sum of the vectors \(\vec{a}\) and \(\vec{b}\).
i.e. \(\overrightarrow{OP}\) + \(\overrightarrow{OQ}\) = \(\overrightarrow{OR}\)
or \(\vec{a}\) + \(\vec{b}\) = \(\overrightarrow{OR}\)
This method of addition of two vectors is called Parallelogram law of addition of vectors.
Properties of Vector Addition
(i) \(\vec{a}\) + \(\vec{b}\) = \(\vec{b}\) + \(\vec{a}\) (Commutative)
(ii) (\(\vec{a}\) + \(\vec{b}\)) + \(\vec{c}\) = \(\vec{a}\) + (\(\vec{b}\) + \(\vec{c}\)) (associativity)
(iii) \(\vec{a}\) + 0 = 0 + \(\vec{a}\) (additive identity)
(iv) \(\vec{a}\) + (-\(\vec{a}\)) = 0 (additive inverse)