What are Disjoint Sets – Venn Diagram and Examples

Here you will learn what are disjoint sets in set theory with venn diagram and examples.

Let’s begin –

What are Disjoint Sets ?

Definition : Two set A and B are said to be disjoint, if \(A \cap B\) = \(\phi\).

If \(A \cap B\) \(\ne\) \(\phi\), then A and B are said to be intersecting or overlapping sets.

Also Read : Formulas and Operation of Sets

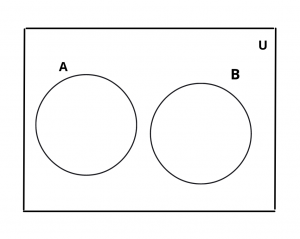
Example : If A = {1, 2, 3, 4, 5, 6}, B = {7, 8, 9, 10, 11} and C = {6, 8, 10, 12, 14}. Then find which of the following two set are disjoint.

Solution : We have sets A, B and C,

Taking intersection of set A and B,

\(A \cap B\) = \(\phi\)

Hence, A and B are Disjoint Sets.

Now, \(A \cap C\) = {6}

Since A intersection C is not \(\phi\). So, they are intersecting sets.

Now, \(B \cap C\) = {8, 10}

Since B intersection C is also not \(\phi\). So, they are also intersecting sets.