Here, you will learn modulus function and what is the domain and range of modulus function.
Let’s begin –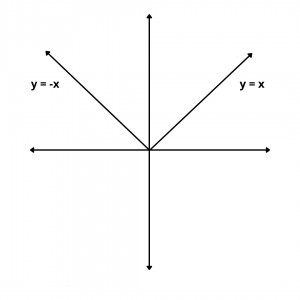
The function f(x) defined by
y = |x| = \(\begin{cases} x & \text{if}\ x \ge 0 \\ -x & \text{if}\ x < 0 \end{cases}\)
is called the modulus function.
It is also called absolute value function.
we observe that the domain of the modulus function is the set R of all real numbers and the range is the set of all non-negative real numbers.
Domain and Range of Modulus Function
For f(x) = |x|,
Domain is R
Range is [0,\(\infty\)]
The graph of the modulus function is as shown in figure, for x > 0, the graph coincides with the graph of the identity function i.e. the line y = x and for x > 0, it is coincident to the line y = -x,
The modulus function has the following properties :
(i) For any real number x, we have
\(\sqrt{x^2}\) = |x|
For example, \(\sqrt{cos^2x}\) = | cos x | = \(\begin{cases} cos x , & 0 \ge x \le \pi/2 \\ -cos x , & \pi/2 < x \le \pi \end{cases}\)
(ii) If a, b are positive real numbers, then
\(x^2\) \(\le\) \(a^2\) \(\iff\) |x| \(\le\) a \(\iff\) -a \(\le\) x \(\le\) a
\(x^2\) \(\ge\) \(a^2\) \(\iff\) |x| \(\ge\) a \(\iff\) x \(\le\) -a or, x \(\ge\) a
\(x^2\) < \(a^2\) \(\iff\) |x| < a \(\iff\) -a < x < a
\(x^2\) > \(a^2\) \(\iff\) |x| > a \(\iff\) x < -a or, x > a
\(a^2\) \(\le\) \(x^2\) \(\le\) \(b^2\) \(\iff\) a \(\le\) |x| \(\le\) b \(\iff\) x \(\in\) [-b, -a] \(\cup\) [a, b]
\(a^2\) < \(x^2\) < \(b^2\) \(\iff\) a < |x| < b \(\iff\) x \(\in\) (-b, -a) \(\cup\) (a, b)
(iii) For any real number x and y, we have
| x + y | = | x | + | y |, if (x \(\ge\) 0 and y \(\ge\) 0) or, (x < 0 and y < 0)
| x – y | = | x | – | y |, if (x \(\ge\) 0 and | x | \(\ge\) | y |) or, (x \(\ge\) 0 and y \(\le\) 0 and | x | \(\ge\) | y |)
| x \(\pm\) y | \(\le\) | x | + | y |
| x \(\pm\) y | > | | x | – | y | |
Hope you learnt what is the domain and range of modulus function, learn more concepts of function and practice more questions to get ahead in the competition. Good luck!