Here you will learn what is the symmetric difference of two sets with venn diagram and examples.
Let’s begin –
Symmetric Difference of Two Sets
Definition : Let A and B be two sets. The symmetric difference of sets A and B is the set (A – B) \(\cup\) (B – A) and is denoted by \(A \Delta B\).
Thus, \(A \Delta B\) = (A – B) \(\cup\) (B – A) = {x : x \(\in\) A \(\cap\) B}
Also Read : Formulas and Operation of Sets
Venn Diagram :
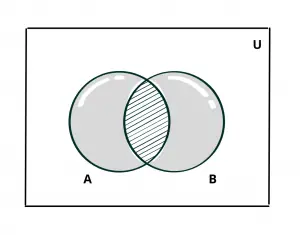
The grey coloured region in the above figure represents \(A \Delta B\).
Example : If A = {1, 2, 3, 4, 5, 6, 7, 8} and B = {1, 3, 5, 6, 7, 8, 9}. then find \(A \Delta B\).
Solution : We have sets A and B,
A – B = {2, 4} and B – A = {9}
\(\therefore\) \(A \Delta B\) = (A – B) \(\cup\) (B – A) = {2, 4, 9}
Example : If A = {x \(\in\) R : 0 < x < 3} and B = {x \(\in\) R : 1 \(\le\) x \(\le\) 5}. then find \(A \Delta B\).
Solution : We have sets A and B,
A – B = {x \(\in\) R : 0 < x < 1}
B – A = {x \(\in\) R : 3 \(\le\) x \(\le\) 5}
\(\therefore\) \(A \Delta B\) = (A – B) \(\cup\) (B – A) = {x \(\in\) R : 0 < x < 1} \(\cup\) {x \(\in\) R : 3 \(\le\) x \(\le\) 5}
\(\implies\) \(A \Delta B\) = {x \(\in\) R : 0 < x < 1 or 3 \(\le\) x \(\le\) 5}