Here you will learn formula for the curved surface area and total surface area of cone and its derivation with examples.
Let’s begin –
What is Cone ?
A cone is a solid which has a circle at its base and a slanting lateral surface that converges at the apex. Its dimensions are defined by the radius of the base (r), the height (h) and the slant height (l)
Formula for Surface Area of Cone
(i) Curved Surface Area (CSA)
curved surface area of cone = \(\pi rl\)
where l is the slant height.
(ii) Total Surface Area (TSA)
Total surface area of cone = CSA + \(\pi r^2\) = \(\pi rl\) + \(\pi r^2\)
Note :
\(l^2\) = \(r^2\) + \(h^2\). Here h is the height of the cone.
This is the relation between slant height and height of cone.
Derivation of the Surface Area of Cone
Take a paper cone and cut one piece of triangle from it along its slant height. It looks like the second picture.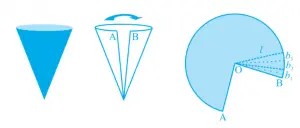
Now, If you further cut the into little pieces along the lines drawn from the point O, each cut portion is almost a small triangle, whose height is the slant height \(l\) of the cone.
Now the area of each triangle = \(1\over 2\) \(\times\) area of triangle \(\times\) \(l\)
So, area of the entire cone = sum of the areas of all the triangles
= \(1\over 2\) \(\times\) (length of entire curved boundary) \(\times\) \(l\)
But length of entire curved boundary makes up the perimeter of the base of the cone and the circumference of the base of the cone = 2πr, where r is the base radius of the cone.
So, Curved surface area = \(1\over 2\) \(\times\) \(2\pi r\) \(\times\) \(l\) = \(\pi rl\)
Now if the base of the cone is to be closed, then a circular piece of paper of radius r is also required whose area is \(\pi r^2\)
So, Total surface area = \(\pi rl\) + \(\pi r^2\) = \(\pi r(l + r)\)
Example : The height of a cone is 16 cm and its base radius is 12 cm. Find the curved surface area and the total surface area of the cone.
Solution : Here, h = 16 cm and r = 12 cm
So, \(l^2\) = \(r^2\) + \(h^2\) \(\implies\) \(l^2\) = 144 + 256 = 400
\(\implies\) \(l\) = 20
So, Curved Surface area = \(\pi rl\) = 3.14 \(\times\) 12 \(\times\) 20
CSA = 753.6 \(cm^2\)
Total surface area = CSA + \(\pi r^2\) = 753.6 + 3.14 \(\times\) 12 \(\times\) 12
TSA = 753.6 + 412.6 = 1205.76 \(cm^2\)