Solution :
In right angled triangle ABC,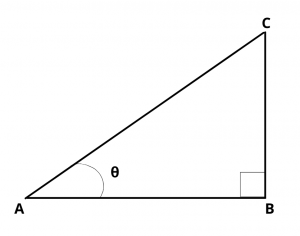
\(sin \theta\) = \(BC\over AC\) \(\implies\) \(sin^2 \theta\) = \(BC^2\over AC^2\)
\(cos \theta\) = \(AB\over AC\) \(\implies\) \(cos^2 \theta\) = \(AB^2\over AC^2\)
On adding,
\(sin^2 \theta\) + \(cos^2 \theta\) = \(BC^2\over AC^2\) + \(AB^2\over AC^2\)
\(sin^2 \theta\) + \(cos^2 \theta\) = \(BC^2 + AB^2\over AC^2\) = \(AC^2\over AC^2\) = 1
[ By Pythagoras theorem, \(AC^2\) = \(BC^2 + AB^2\) ]
\(\implies\) \(sin^2 \theta\) + \(cos^2 \theta\) = 1